Trigonometrische Funktionen – die beliebtesten Themen
Welche Arten von trigonometrischen Funktionen gibt es?
Es gibt verschiedene trigonometrische Funktionen. Häufig können dir Koordinatensysteme begegnen, die eine andere x-Achseneinteilung haben. Die Achse wird dabei in Vielfachen von \(\pi\) dargestellt. Lass dich davon aber nicht verunsichern.
Sinusfunktion
Die wohl bekannteste trigonometrische Funktion ist die Sinusfunktion. Die Sinusfunktion erweitert den von rechtwinkligen Dreiecken bekannten Sinus eines Winkels \(\sin(\alpha)\) auf eine Funktion im ganzen reellen Zahlenbereich \(\mathbb{R}\).

Kosinusfunktion
Außerdem ist die Kosinusfunktion für das Thema wichtig. Auch diese Funktion erweitert den bekannten Kosinus aus dem rechtwinkligen Dreieck \(\cos(\alpha)\) auf eine Funktion im ganzen reellen Zahlenbereich \(\mathbb{R}\).
Wichtig ist, dass mithilfe von Verschiebung die Sinusfunktion in die Kosinusfunktion überführt werden kann. Du kannst aber auch die Kosinusfunktion in die Sinusfunktion überführen, indem du die Kosinusfunktion entweder um \(\displaystyle \frac \pi 4\) nach rechts oder um \(\displaystyle \frac {3\pi} 4\) nach links verschiebst.
Tangensfunktion
Die nächste bekannte trigonometrische Funktion ist die Tangensfunktion. Diese ist grafisch gänzlich anders aufgebaut. Die Tangensfunktion verläuft periodisch, jedoch nicht zusammenhängend, sondern es sieht so aus, als wenn nach jeder Länge von \(\pi\) eine neue Kurve beginnt.

Welche Eigenschaften von trigonometrischen Funktionen sind wichtig?
Die trigonometrischen Funktionen haben besondere Eigenschaften. Die Eigenschaften, die im Folgenden angesprochen werden, sind für die Analyse der Funktion sehr wichtig.
Einteilung der x-Achse
Die x-Achse wird bei den trigonometrischen Funktionen häufig anders eingeteilt, als du es gewohnt bist. Wichtig ist hierbei die Zahl \(\pi\). Die Nullstellen, Extremstellen und auch sonst alle Punkte basieren alle auf einem Vielfachen von \(\pi\).
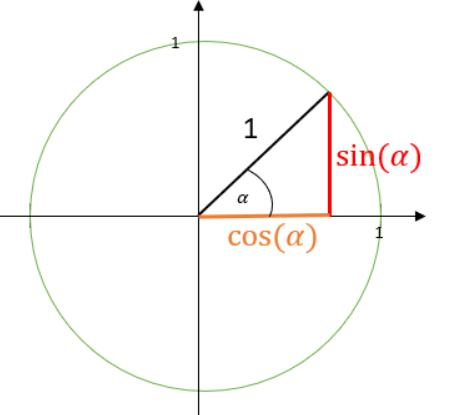
Um zu verstehen, warum das so ist, müssen wir uns den sogenannten Einheitskreis näher ansehen.
Die trigonometrischen Funktionen ordnen einem Winkel ein passendes Seitenverhältnis zu. Aus der Trigonometrie weißt du, wie man diese Seitenverhältnisse berechnet. Wie sich diese Formeln ableiten, kannst du im Einheitskreis erkennen.
Hast du nun so ein Seitenverhältnis gegeben, kannst du auch den passenden x-Wert berechnen.
Periodizität, Nullstellen und Extremstellen
Eine andere wichtige Eigenschaft ist die Periodizität. Diese gibt an, dass sich die Werte einer Funktion nach einem konstanten Abstand immer wieder wiederholen. Die Sinus-, Kosinus- und Tangensfunktionen sind periodisch.
In der Grafik kannst du die Sinusfunktion erkennen. Die blauen Kreise zeigen, wo die Extremstellen (Maxima und Minima) zu finden sind. Die grünen Kreise zeigen die Nullstellen der Sinusfunktion. Wie du siehst, wiederholen sich die Nullstellen alle \(\pi\)-Längeneinheiten. Auch eine Extremstelle tritt immer wieder nach \(\pi \)-Längeneinheiten auf. Dabei wechseln sich die Maxima und Minima ab. Die Tangensfunktion hat allerdings keine Extremstellen.

Amplitude
Auch die Amplitude ist wichtig, um den Verlauf der Funktionen besser zu verstehen. Einfach gesagt ist die Amplitude der größte Abstand (größter y-Wert) zur x-Achse. Die Funktionen \(\sin(x)\) und \(\cos(x)\) haben eine Amplitude von \(1\).

Symmetrie
Die Symmetrie ist die nächste Eigenschaft, die betrachtet werden muss. Eine Funktion kann punkt- oder achsensymmetrisch sein. Die Sinus- und Tangensfunktion ist punktsymmetrisch und die Kosinusfunktion ist achsensymmetrisch zur y-Achse.
Monotonie
Auch die Monotonie kann bei trigonometrischen Funktionen betrachtet werden. Die Sinus- und Kosinusfunktionen wechseln die Monotonie zwischen den Extremstellen. Die Tangensfunktion ist im gesamten Definitionsbereich streng monoton steigend.
Umkehrfunktionen
Die Umkehrfunktionen sind die sogenannten Arcusfunktionen. Auf dem Taschenrechner findest du sie häufig in Kombination mit dem Exponenten \(-1\) (zum Beispiel \(\sin ^{-1}\)).
Wo gibt es trigonometrische Funktionen noch?
Die trigonometrische Funktionen hat eine große Bedeutung in der Geometrie. Außerdem findest du diese auch oft in den naturwissenschaftlichen Bereichen.
Trigonometrische Funktionen in der Geometrie
Trigonometrische Funktionen kennst du ursprünglich aus dem Themengebiet rechtwinklige Dreiecke.
Die trigonometrischen Funktionen kannst du darstellen mit:
\(\sin(\alpha)=\frac{\text{Gegenkathete}}{\text{Hypotenuse}}\), \(\cos(\alpha)=\frac{\text{Ankathete}}{\text{Hypotenuse}}\) und \(\tan(\alpha)=\frac{\text{Gegenkathete}}{\text{Ankathete}}\)
Diese Seitenverhältnisse kannst du auch im Einheitskreis nachvollziehen.
Trigonometrische Funktionen in den Naturwissenschaften
Es gibt zahlreiche Realbeispiele. Alle Vorgänge, die sich wiederholen oder im Kreis bewegen, kann man mathematisch durch trigonometrische Funktionen darstellen. Viele davon spielen sich in der Physik und Biologie ab. Ein Beispiel sind Wellen, wie z. B. Tonwellen. Wenn du Musik aufnimmst, um zu überprüfen, welches Lied das ist, werden grafisch Kurven benutzt, um die Töne darzustellen. Das passiert durch Überlagerung von trigonometrischen Funktionen.

