Was ist eine Exponentialfunktion?

Eine Exponentialfunktion ist eine Funktion, die im einfachsten Fall die Form \(f(x) = a^x\) hat. Dabei ist die Basis \(a\) eine reelle positive Zahl ungleich \(0\) oder \(1\) und der Exponent \(x\) eine Variable. Wie die meisten Funktionen hat auch die Exponentialfunktion einen charakteristischen Graphen. Dieser lässt sich durch Parameter beeinflussen.

Exponentialfunktionen werden dich bis in die Oberstufe begleiten und du musst diese von anderen Funktionstypen, wie zum Beispiel den linearen Funktionen, unterscheiden können. Sie sind ein wichtiger Bestandteil der Abiturprüfungen.

In den folgenden Abschnitten werden ihre wichtigsten Eigenschaften und ihre Bedeutung in der Welt kurz erklärt. Einige Lernwege sowie Klassenarbeiten findest du direkt unter diesem Abschnitt.

Exponentialfunktionen – die beliebtesten Themen

alle Klassenarbeitenalle Themen mit Videos und Übungen

Welche Arten von Exponentialfunktionen gibt es?

Es gibt unterschiedliche Arten von Exponentialfunktionen. Drei wichtige werden dir hier vorgestellt:

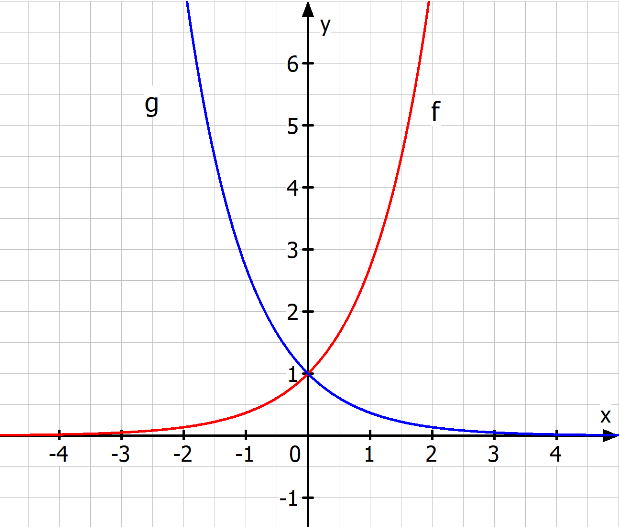
  • Wachstumsfunktionen sind monoton steigende Funktionen, die Vorgänge beschreiben, bei denen etwas zunimmt. In der Grafik entspricht das der Funktion \(f\).
  • Zerfallsfunktionen sind monoton fallende Funktionen, die Vorgänge beschreiben, bei denen etwas abnimmt. In der Grafik entspricht das der Funktion \(g\).
  • Die natürliche Exponentialfunktion ist eine Funktion, die als Basis die eulersche Zahl \(e\) hat. Sie beschreibt wachsende Vorgänge und zugleich ihre momentanen Änderungsraten.

Die Eigenschaft der natürlichen Exponentialfunktion stellt in der Funktionsanalyse einen wichtigen Vorteil dar. Deshalb werden häufig mithilfe von Logarithmusfunktionen gewöhnliche Exponentialfunktionen in natürliche umgewandelt. Um dies durchführen zu können, musst du dich mit e-Funktionen und den Rechenregeln der Logarithmusfunktionen gut auskennen.

Zwei Exponentialfunktionsgraphen in einem Koordinatensystem.

 

Welche Eigenschaften von Exponentialfunktionen sind wichtig?

Wie du dies schon von linearen oder quadratischen Funktionen weißt, haben Funktionstypen bestimmte Eigenschaften. Das gilt natürlich auch für Exponentialfunktionen. Sie haben einen typischen Kurvenverlauf und Parameter, die diesen beeinflussen.

Einschränkung der Basis \(a\)

Bei Exponentialfunktionen spielt die Basis eine wichtige Rolle. Diese darf auf keinen Fall negativ sein. Auch \(0\) und \(1\) eignen sich nicht. Das hat unterschiedliche Gründe:

  • Betrachten wir zum Beispiel die Exponentialfunktion \(f(x) = (-4)^x\). Setzen wir \(x = \frac{1}{2}\), so muss die Wurzel von \(-4\) gezogen werden. Diese ist jedoch nicht definiert.
  • Ist auf der anderen Seite die Basis gleich eins, so haben wir eine konstante Funktion. Dasselbe gilt für eine Basis gleich null.

Einfluss der Parameter auf die Exponentialfunktionen

Der Graph von Exponentialfunktionen sieht für gewöhnlich so aus, dass er sich in einem Quadranten dem Wert null asymptotisch annähert und in dem anderen gegen unendlich strebt.

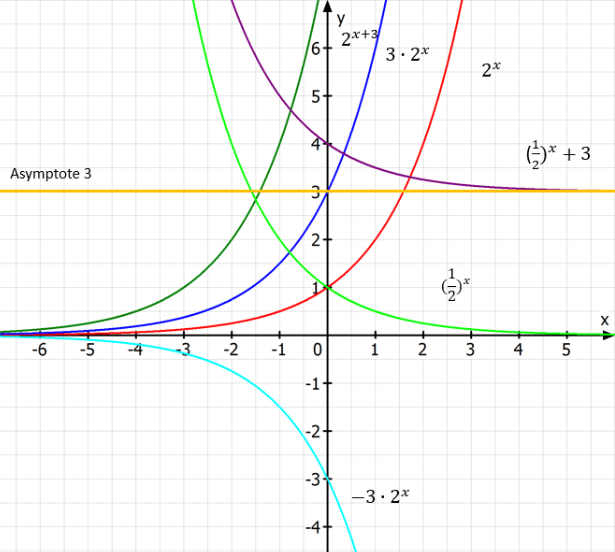
Nun gibt es Parameter, die die Funktion stark beeinflussen. Eine Exponentialfunktion lässt sich auch allgemein durch die Formel \(f(x) = b \cdot a^{c \cdot x + d} + e\) darstellen. Neben der Aufzählung findest du die möglichen Einflüsse grafisch dargestellt.

  • Die Basis \(a\) bildet den Kern der Funktion. Sie beeinflusst sowohl ihre Schnittstelle mit der y-Achse als auch ihr Wachstum.
  • Der Faktor \(b\) gibt die Schnittstelle mit der y-Achse an. Werden Wachstums- oder Zerfallsprozesse beschrieben, wird der Faktor auch Anfangsbestand genannt. Natürlich ist dieser auch ausschlaggebend für die Steigung der Funktion.
  • Der Exponentialfaktor \(c\) beeinflusst die Steigung und Monotonieeigenschaften der Funktion.
  • Die Konstante \(d\) sorgt für eine Verschiebung der Funktion entlang der x-Achse.
  • Die Konstante \(e\) beschreibt die Verschiebung der Asymptote entlang der y-Achse.
verschiedene e-Funktionen

Wo finde ich Exponentialfunktionen noch?

Exponentialfunktionen werden in der Schule deshalb so intensiv behandelt, weil sie sehr häufig in unterschiedlichen Bereichen der Forschung und Wirtschaft genutzt werden. Mit ihnen lassen sich Prozesse modellieren und Aussagen über die Zukunft und Vergangenheit treffen. Im Folgenden werden zwei Beispiele dafür betrachtet, die auch im Unterricht oft bearbeitet werden.

Bakterielles Wachstum

Bakterien sind Mikroorganismen, die sich in bestimmten Zeiträumen durch Zweiteilung fortpflanzen. So kann berechnet werden, wie viel Bakterien nach mehreren Stunden existieren. Außerdem lässt sich mit dem Wissen über die Wachstumsrate, die vergangene Zeit und den momentanen Bestand auch der Anfangsbestand einer Bakterienkultur bestimmen.

Zinsen

Stell dir vor, du eröffnest bei einer Bank ein Sparkonto und zahlst einmalig einen bestimmten Betrag ein. Die Bank gibt an, monatlich dein Guthaben zu verzinsen. Das bedeutet, dass dir jeden Monat ein prozentualer Betrag deines angelegten Geldes gutgeschrieben wird. Dieser Vorgang lässt sich durch exponentielles Wachstum simulieren. So kannst du zum Beispiel ermitteln, wie lange du das Geld nicht anrühren darfst, bis du dir ein Fahrrad leisten kannst. Hierbei ist wichtig, dass du exponentielles und lineares Wachstum unterscheiden kannst.

Das geht natürlich auch umgekehrt. So nehmen Banken für Kredite Zinsen, die man zusammen mit dem Kreditbetrag zurückzahlen muss. Je länger die Rückzahlung braucht, desto mehr muss insgesamt bezahlt werden.