Was du wissen musst
-
Wann kann man Brüche kürzen?
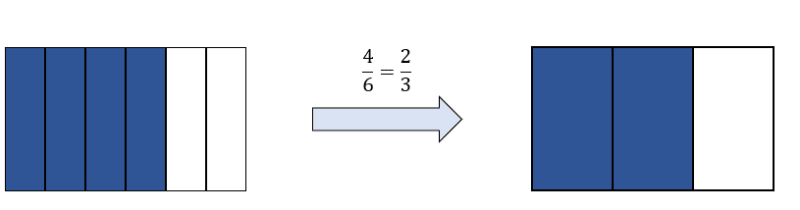
Du kannst einen Bruch genau dann kürzen, wenn Zähler und Nenner einen gemeinsamen Teiler haben. Den Bruch \(\frac{4}{6}\) kannst du mit \(2\) kürzen, da sowohl \(4\) als auch \(6 \) ohne Rest durch \(2\) geteilt werden können. Somit erhältst du:
\(\frac{4}{6} = \frac{4\ :\ 2}{6\ :\ 2} = \frac{2}{3}\)
Bei diesem Bruch hat sich nur das Aussehen geändert. Der Wert des Bruchs bleibt gleich.
Es gibt auch Brüche, die du nicht mehr kürzen kannst. In diesem Fall haben Nenner und Zähler keinen gemeinsamen Teiler, wie zum Beispiel \(\frac{7}{15}\).
-
Wie erweitert man Brüche?
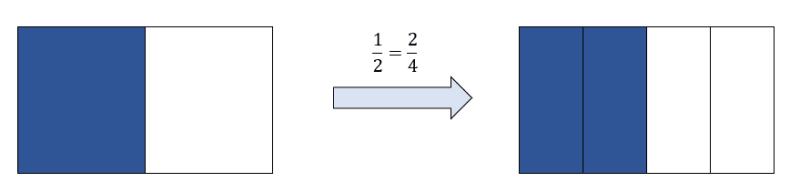
Beim Erweitern multiplizierst du Zähler und Nenner mit einer Zahl. Den Bruch \(\frac{1}{3}\) kannst du zum Beispiel mit \(6\) erweitern.
\(\frac{1}{3} = \frac{1\ \cdot\ 6}{3\ \cdot\ 6} = \frac{6}{18}\)Du musst nur aufpassen, dass du Zähler und Nenner mit der gleichen Zahl multiplizierst. Jetzt fragst du dich bestimmt, wann man Brüche erweitern kann? Du kannst jeden Bruch mit jeder ganzen Zahl erweitern.
Denk daran, dass sich der Wert eines Bruchs beim Erweitern nicht verändert. Er sieht am Ende zwar anders aus, bleibt aber gleich groß.
-
Wofür muss man Brüche kürzen und erweitern können?
Zum einen musst du Brüche kürzen und erweitern, um sie miteinander vergleichen und ordnen zu können. Bei den Brüchen \(\frac{33}{45}\)und \(\frac{12}{15}\) ist nicht direkt klar, welcher Bruch größer ist. Kürzen wir \(\frac{33}{45}\) mit \(3\), erhalten wir:
\(\frac{33}{45} = \frac{33\ :\ 3}{45\ :\ 3} = \frac{11}{15} \)
Jetzt siehst du gleich, dass der Bruch \(\frac{12}{15}\) größer als der Bruch \(\frac{33}{45}\) ist.
Außerdem ist das Kürzen und das Erweitern wichtig, um Verhältnisse zu erkennen und zu beschreiben. Wenn du zum Beispiel in den Nachrichten folgende Meldung hörst: „Ein Fünftel der Autofahrer fährt schneller als im vergangenen Jahr. Im letzten Monat sind sogar zwei Drittel schneller gefahren“, dann weißt du genau, wie viel das im Vergleich zueinander ist.
Außerdem kannst du Brüche addieren und subtrahieren. Hier musst du die Brüche mit Kürzen oder Erweitern auf den gleichen Nenner bringen. Das führt dich direkt zur nächsten Frage.
-
Wie macht man Brüche gleichnamig?
Am einfachsten machst du Brüche gleichnamig, indem du den Bruch mit dem Nenner des anderen erweiterst. Nehmen wir an, du möchtest \(\frac{3}{4} \) und \( \frac{2}{3}\)vergleichen. Du erweiterst zuerst den linken Bruch mit \(3\).
\(\frac{3}{4} =\frac{3\ \cdot\ 3}{4\ \cdot\ 3} = \frac{9}{12} \)
Anschließend erweiterst du den rechten Bruch mit \(4\). Du nimmst also immer den Nenner des anderen Bruchs.
\(\frac{2}{3} = \frac{2\ \cdot\ 4}{3\ \cdot\ 4} = \frac{8}{12} \)
Nun haben beide Brüche denselben Nenner. \(\frac{3}{4} \) ist also größer als \( \frac{2}{3}\).
Es gibt noch eine andere Methode, Brüche gleichnamig zu machen. Dafür verwendest du das kleinste gemeinsame Vielfache (kgV). Du erweiterst oder kürzt so, dass in beiden Nennern das kleinste gemeinsame Vielfache steht.