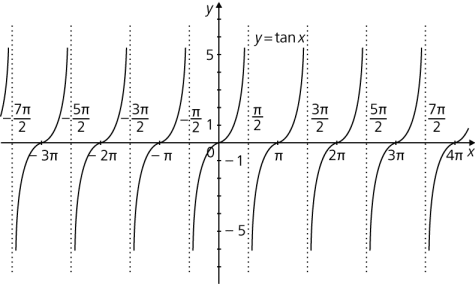
Die Tangensfunktion ist eine trigonometrische Funktion, welche den vom rechtwinkligen Dreieck bekannten Tangens eines Winkels („\(\displaystyle \tan \varphi = \frac{\sin \varphi}{\cos \varphi}\)“) durch Verwendung des Bogenmaßes zu einer auf (fast) ganz \(\mathbb R\) definierten Funktion erweitert. Nur an den Polstellen (siehe unten), also an den Nullstellen der Kosinusfunktion, ist der Tangens nicht definiert. Die maximale Definitionsmenge ist somit \(\displaystyle D_f = \mathbb R \setminus \{x| \left( k + \frac 1 2\right) \cdot \pi , \ k \in \mathbb Z \}\), der Wertebereich ist \(W_f = \mathbb R\).
Die Tangensfunktion ist periodisch, es gilt \(\tan x = \tan(x + k \cdot \pi) \ \ (k \in \mathbb Z)\).
Der Funktionsgraph der Tangensfunktion ist punktsymmetrisch zum Ursprung, sie ist also eine sog. ungerade Funktion. Er ist außerdem auch punktsymmetrisch zu allen Nullstellen (weil die Funktion bis nach „\(\pm \infty\)“ periodisch ist).
Weitere Eigenschaften
- Nullstellen: \(x_k = k \cdot \pi \ \ ( k \in \mathbb{Z})\)
- Polstellen (Unendlichkeitsstellen) und Asymptoten: Die Definitionslücken bei \(\displaystyle x = \left( k + \frac 1 2\right) \cdot \pi \ \ (k \in \mathbb Z )\) sind Polstellen mit \(\displaystyle \lim_{x \to x_k -0} \tan x =+\infty\) und \(\displaystyle \lim_{x \to x_k +0} \tan x =-\infty\). An den Polstellen findet also ein Vorzeichenwechsel statt. Die senkrechten Geraden mit \(\displaystyle x = \left( k + \frac 1 2\right) \cdot \pi \ \ (k \in \mathbb Z )\) sind senkrechte (vertikale) Asymptoten des Funktionsgraphen.
Die Tangensfunktion hat keine Extremstellen, aber jede Nullstelle ist gleichzeitg auch eine Wendestelle. - Monotonie: Die Tangensfunktion ist im gesamten Definitionsbereich streng monoton, d. .h in jedem zwischen zwei Polstellen verlaufenden Ast des Funktionsgraphen, steigend.
Die Ableitung des Tangens ist \(\displaystyle (\tan x)' = 1 + \tan^2 x= \frac {1}{\cos^2 x}\).
Der Kehrwert der Tangensfunktion, wird auch als Kotangensfunktion bezeichnet, \(\displaystyle \cot x = \frac{1}{\tan x}\). Dieser spielt in der Schule aber keine so große Rolle.