Bruchteile

Was du wissen musst

• Welche Eigenschaften von Bruchteilen sind wichtig?

  Ein Bruchteil beschreibt einen Anteil von einem Ganzen. Besonders wichtig ist, dass der Nenner nie \(0\) sein kann. Wenn du nämlich keine Torte hast, kannst du sie auch nicht in Stücke schneiden und aufteilen.

  Ein Bruchteil ist gleichzeitig eine Division.

  Das heißt, du kannst die Bruchzahl \(\frac{1}{2}\) ausrechnen, indem du \(1:2\) rechnest. Du erhältst:
  \(\frac{1}{2}=1:2=0{,}5\)
  Das ist ein weiterer Grund, warum der Nenner niemals \(0\) sein darf: Die Division durch \(0\) gibt es nicht.

  Das Ergebnis \(0{,}5\) ist nicht allein durch \(\frac{1}{2}\) errechenbar. Auch \(\frac{2}{4}=2:4\) oder \(\frac{5}{10}=5:10\) haben als Ergebnis \(0{,}5\). Das heißt, dass die gleiche Bruchzahl verschieden dargestellt werden kann. Dennoch ist es das Gleiche, ob du die Hälfte, zwei Viertel oder fünf Zehntel der Torte isst. Das die Bruchteile \(\frac{1}{2}=\frac{2}{4}=\frac{5}{10}\) gleich groß sind, kannst du nachvollziehen, wenn du die Brüche kürzt und erweiterst.

  Wie passen die natürlichen Zahlen mit den Bruchzahlen zusammen?

  Eine weitere Besonderheit ist, dass die natürlichen Zahlen spezielle Bruchzahlen sind. Ihr Nenner ist \(1\). Da es sich also um eine Division durch \(1\) handelt, kann man den Nenner auch einfach weglassen und somit Zeit und Platz sparen. Zum Beispiel:
  \(\frac{5}{1}=5:1=5\)

• Wie erkennt man Bruchteile und stellt sie dar?

  Bruchteile kommen ins Spiel, sobald du dir etwas mit jemandem teilst. Die Frage lautet dann, wie groß der Anteil ist, den du bekommst, und wie du ihn angibst.

  Um ein Blech Kuchen zu teilen, schneidest du den Kuchen zunächst in gleich große Stücke. Du nimmst dir \(2\) Stücke davon. Deinen Anteil am Kuchen kannst du nun mit Bruchteilen angeben. Dafür zählst du, in wie viele Teile der Kuchen insgesamt geteilt worden ist. Diese Zahl schreibst du dann in den Nenner (\(\frac{}{20}\)). Die Anzahl an Stücken, die du genommen hast, schreibst du in den Zähler (\(\frac{2}{20}\)). Das ist dein Anteil am Kuchen.

  

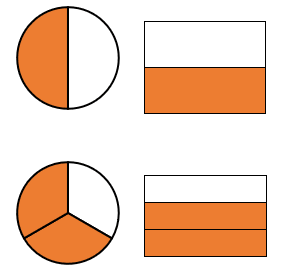
  Wenn du Anteile darstellen möchtest, gehst du fast genauso vor: Um die Hälfte (\(\frac{1}{2}\)) oder zwei Drittel (\(\frac{2}{3}\)) von einem Ganzen zu markieren, musst du das Ganze zunächst in so viele Stücke teilen, wie im Nenner angeben sind. Dann markierst du die Anzahl an Stücken, die im Zähler angegeben ist. Welche du markierst, spielt keine Rolle, weil alle Teilstücke gleich groß sind.

  \(\frac{\text{Zähler}}{\text{Nenner}}=\frac{\text{Anzahl der markierten Stücke}}{\text{Anzahl der insgesamten Stücke}}\)

  

   

• Wie berechnet man Bruchteile?

  Mit Bruchteilen kannst du die gleichen Berechnungen wie mit den natürlichen Zahlen durchführen. Du kannst Brüche addieren und subtrahieren sowie multiplizieren und dividieren.

  Der einzige Unterschied zu den Berechnungen mit den natürlichen Zahlen ist, dass du die Bruchteile nur dann sofort addieren oder subtrahieren kannst, wenn der Nenner übereinstimmt. Ist das nicht der Fall, so kannst du durch Erweitern oder Kürzen die Bruchteile auf den gleichen Nenner bringen und dann wie gewohnt addieren oder subtrahieren.

• Wofür braucht man Bruchteile?

  Bruchteile begegnen uns im täglichen Leben. Sei es beim Kochen, Einkaufen oder Musizieren. Zum Beispiel ist es sehr nützlich, wenn du Bruchteile von Größen auf deinem Messbecher umrechnen und berechnen kannst. Du benötigst zum Beispiel einen Dreiviertelliter (\(\frac{3}{4}\ \text{l}\)) Wasser zum Kochen. Wie viel Wasser ist das denn genau?

  Ein Dreiviertelliter Wasser entspricht \(\frac{3}{4}\) von \(1\ \text{l}\). Umgerechnet in Milliliter sind das \(\frac{3}{4}\) von \(1000 \ \text{ml}\) Wasser. Das sind also:
  Liter: \(\frac{3}{4}\cdot 1=3:4=0{,}75\)
  Milliliter: \(\frac{3}{4}\cdot 1000=3000:4=750\) 

  Ebenfalls begegnen dir Bruchteile, wenn du die Tomate in vier Viertel (\(\frac{4}{4}\)) schneidest, eineinhalb (\(1\frac{1}{2}\)) Kilometer läufst, ein halbes Dutzend (\(\frac{6}{12}\)) Eier zum Backen benötigst oder dir in der Musik zwei Sechzehntelnoten ♬ (\(\frac{2}{16}\)) und eine Achtelnote♪(\(\frac{1}{8}\)) begegnen.

  Später sind die Bruchteile sehr nützlich, um Terme und Gleichungen geschickt umzuformen.