Analytische Geometrie – Lernwege
Analytische Geometrie – Klassenarbeiten
Welche Aufgaben gibt es in der analytischen Geometrie?
Die Aufgaben in der analytischen Geometrie beinhalten üblicherweise alle Vektoren im dreidimensionalen Raum. Meist fängst du damit an, erst mal den dreidimensionalen Raum – und in ihm Vektoren, Figuren, Punkte und mehr – zeichnerisch im kartesischen Koordinatensystem darzustellen.
Danach überwiegt der rechnerische Teil und es wird die Vektorrechnung eingeführt. Mit ihr lassen sich sämtliche Themenbereiche ausrechnen und beschreiben. Vieles davon kennst du aus dem zweidimensionalen Raum, zum Beispiel den Abstand zwischen zwei Punkten sowie Schnittpunkt und Winkel von zwei Geraden.
Aber auch die Lage zueinander, die im Zweidimensionalen nur zwei Möglichkeiten hat, wird ausführlich behandelt. Es gibt zum Beispiel bei der Lage zwischen Geraden neben „sie schneiden sich“ und „sie sind parallel zueinander“ im Dreidimensionalen auch die Möglichkeit, dass sie windschief sind.
Wie zeichnet man Vektoren im dreidimensionalen Koordinatensystem?
Vektoren bestehen im Dreidimensionalen aus drei Koordinaten. In der Ebene hat ein Punkt \(P\) die Koordinaten \(P(x|y) \). In drei Dimensionen haben ein Punkt \(P(x\,| \,y\, |\, z)\) und ein Vektor \(\vec{v}=\begin{pmatrix} x\\ y \\ z\end{pmatrix}\) drei Koordinaten, die dritte ist die Koordinate \(z\). Auch gängig ist, dass die Koordinaten nicht mit \(x\), \(y\) und \(z\), sondern als \(x\) mit Index angegeben sind. Dann sähen die Koordinaten des Vektors \(\vec{v}\) so aus: \(\vec{v}=\begin{pmatrix} x_1\\ x_2 \\ x_3\end{pmatrix}\)
Ein dreidimensionales Koordinatensystem sieht so aus:
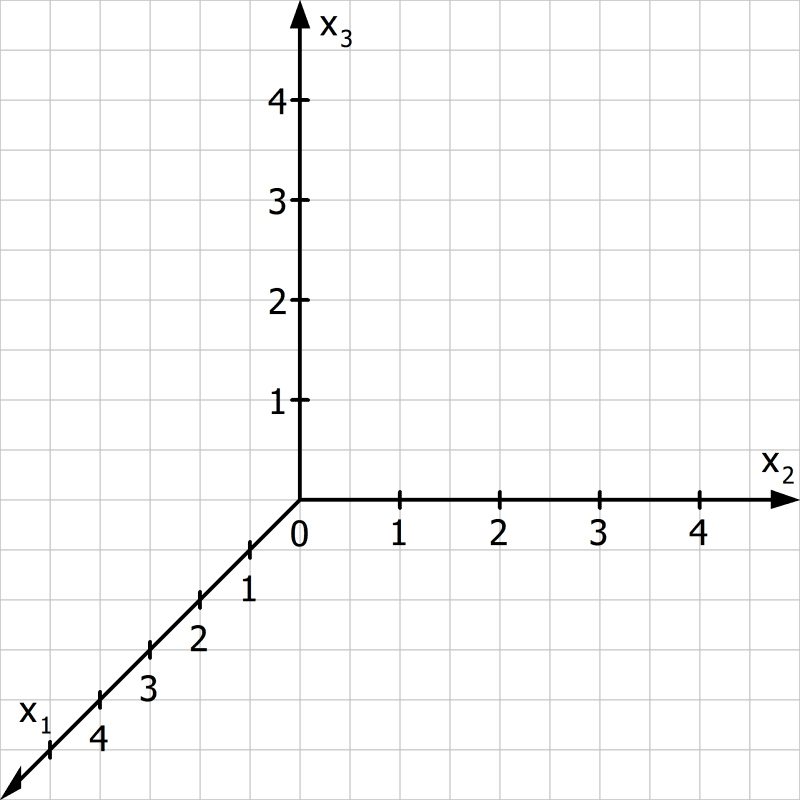
Wie du siehst, ist die neue Achse im \(45^°\)-Winkel zu den anderen gezeichnet. Außerdem fällt auf, dass ein diagonaler Abstand zwei horizontalen oder vertikalen Kästchenbreiten entspricht.
Um in einem dreidimensionalen Koordinatensystem Punkte zu finden, gehst du nun nach und nach die einzelnen Koordinaten ab. Bei einem Punkt \(P= (1|2|3)\) gehst du zuerst einen Schritt in \(x\)-Richtung, dann \(2\) Schritte in \(y\)-Richtung und zuletzt \(3\) in \(z\)-Richtung. Da du das Ganze auf einem zweidimensionalen Objekt (Papier) darstellst, kann es anfangs schwierig sein. Mit der Zeit wirst du dich aber an diese Darstellung gewöhnen.
Vektoren zeichnest du ähnlich, und zwar indem du zuerst den Anfang und dann den Endpunkt findest und sie dann verbindest. Vektoren haben immer eine Richtung. Zum Beispiel verläuft der Vektor \(\vec{0P}=\begin{pmatrix}1\\2\\3\end{pmatrix}\) von \(0=(0\,|\,0\,|\,0)\) zu \(P\) – und nicht andersherum. Hierbei kann es helfen, Vektoren zeichnen zu üben.
Wie rechnet man mit Vektoren?
Beim Rechnen mit Vektoren ist es ähnlich wie beim Zeichnen: Einiges ist gleich, doch ein paar Dinge ändern sich. Es gibt Besonderheiten, sodass du bestimmte Dinge nicht oder anders als bei reellen Zahlen durchführst. Zum Beispiel kannst du keine Wurzel aus einem Vektor ziehen. Auch gibt es zwei neue Produkte, die ausschließlich für Vektoren benutzt werden.
Vektoren werden koordinatenweise miteinander addiert und subtrahiert, das heißt, die erste Koordinate von Vektor \(\vec{a}\) addierst du mit der ersten Koordinate von Vektor \(\vec{b}\). Das ergibt dann die erste Koordinate des Vektors \(\vec{c}=\vec{a}+\vec{b}\).
Du kannst keine reellen Zahlen mit Vektoren addieren oder subtrahieren. Allerdings kannst du Vektoren mit reellen Zahlen multiplizieren (und damit auch durch reelle Zahlen teilen, indem du mit dem Kehrwert multiplizierst). Bei der Multiplikation werden alle Koordinaten mit dem Faktor multipliziert; der Faktor wird allgemein als Skalar bezeichnet.
Die oben genannten neuen Produkte sind das Skalarprodukt und das Kreuzprodukt. Das Skalarprodukt gibt an, ob Vektoren im rechten Winkel zueinander stehen. Das Kreuzprodukt erzeugt einen Vektor, der im rechten Winkel zu den beiden Vektoren steht, die du im Kreuzprodukt multiplizierst.
