Die Logarithmusfunktion \(f : x \mapsto f(x) = \log_a x\) bildet jede positive reelle Zahl x auf ihren Logarithmus zur (positiven) Basis a ab. Dabei ist allerdings a = 1 ausgeschlossen, da in diesem Fall der Logarithmus nicht sinnvoll definiert werden kann.
Die maximale Definitionsmenge ist \(D_f = \mathbb R^+\), die Wertemenge ist dann \(W_f = \mathbb R\).
Achtung: Der Logarithmus ist für negative Argumente oder für x = 0 nicht definiert. Daher muss man bei Funktionen, die einen Logarithmus-Term enthalten, immer darauf achten, dass dessen Argument positiv bleibt. Andernfalls muss man die Definitionsmenge entsprechend einschränken oder man hat es mit einer Definitionslücke zu tun!
Beispiele:
Die Logarithmusfunktionen sind die Umkehrfunktionen der Exponentialfunktionen: \(y = \log_a x \ \ \Leftrightarrow \ \ x = a^y\).
Eigenschaften von Logarithmusfunktionen
Die Logarithmusfunktionen sind eine Funktionenschar mit dem Parameter a, ihre Eigenschaften hängen zum Teil wesentlich von diesem Parameter ab:
-
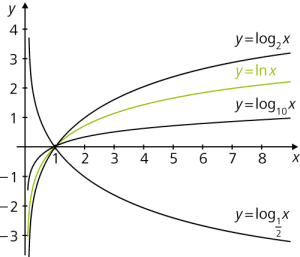
Alle Logarithmusfunktionen haben genau eine Nullstelle an der Selle x = 1, der Punkt (1|0) ist der einzige gemeinsame Punkt aller Funktionsgraphen.
-
Es gibt weder Extrem- noch Wendestellen.
-
Die Logarithmusfunktionen sind in ganz \(\mathbb{R}^+\) für 0 < a < 1 streng monoton fallend, für a > 1 streng monoton steigend.
-
Die y-Achse (x = 0) ist für alle Logarithmuskurven eine vertikale Asymptote. Auch wenn die Graphen für große x-Werte immer flacher werden, gibt es trotzdem keine horizontale Asymptote: Für 0 < a < 1 ist \(\displaystyle \lim_{x \to \infty}\log_{a}x = - \infty\) und für a > 1 \(\displaystyle \lim_{x \to \infty}\log_{a}x = + \infty\).
-
Es gelten allerdings die folgenden Grenzwerte: \(\displaystyle \lim_{x \to 0+0} x\log_{a}x = \lim_{x \to \infty} \frac{ \log_{a}x }{x^p} = 0 \ \ (p \in \mathbb R^+)\). Dies kann man so interpretieren, dass der Logarithmus „langsamer“ als jede Potenz gegen unendlich geht.
-
Die Graphen mit den Funktionsgleichungen \(\displaystyle y = \log_a x\) und \(\displaystyle y = \log_{\frac{1}{a}} x\) sind zueinander symmetrisch bezüglich der x-Achse.
-
Die Ableitung des natürlichen Logarithmus (mit der Basis e, also der Euler’schen Zahl) ist die antiproportionale Funktion (Kehrwertfunktion):
\(\displaystyle (\ln x)' = \frac 1 x\) und damit \(\displaystyle \int \frac 1 x \text dx = \ln x\).