Eine Asymptote ist eine Gerade (oder allgemeiner eine Kurve) an die sich ein gegebener Funktionsgraph an den Rändern des Definitionsbereichs beliebig dicht, aber niemals exakt annähert, also entweder für \(x \to \pm\infty\) oder in der Umgebung einer Polstelle (Unendlichkeitsstelle). Das Wort Asymptote kommt aus dem Griechischen und bedeutet „die Nichtzusammenfallende“ (besser wäre allerdings „Fast-aber-nicht-ganz-Zusammenfallende“)
Man hat es in der Schule vor allem mit drei Arten von Asymptoten zu tun:
- Waagerechte (horizontale) Asymptote: Wenn für eine Funktion der Grenzwert \(\displaystyle \lim_{x\to\pm\infty}f(x) = g\) existiert, dann ist die waagerecht, also parallel zur x-Achse verlaufende Gerade y = g eine waagerechte Asymptote.
Beispiel:
Für die antiproportionale Funktion \(f(x) = \dfrac1 x\) ist \(\displaystyle \lim_{x\to\pm\infty}f(x) = 0\), also hat sie die x-Achse (y = 0) als waagerechte Asymptote.
- Senkrechte (vertikale) Asymptote: Wenn eine Funktion an einer Polstelle xP divergiert, also den uneigentlichen Grenzwert \(\displaystyle \lim_{x\to x_\text P}f(x) = \pm \infty\) hat, dann besitzt sie dort eine senkrecht, d. h. parallel zur y-Achse verlaufende Asymptote, nämlich die Gerade x = xP.
Beispiel:
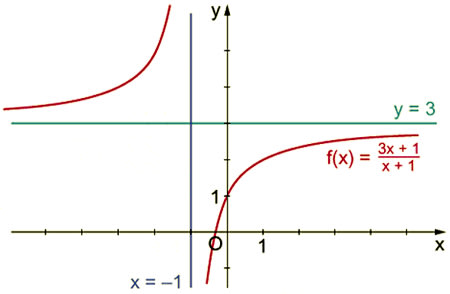
Die gebrochenrationale Funktion \(f(x) = \dfrac{3x + 1}{x + 1}\) hat bei x = –1 eine Polstelle, also eine senkrechte Asymptote. Außerdem hat sie bei y = 3 auch eine waagerechte Asymptote.
- Schräge (schiefe) Asymptote: Wenn eine Funktion sich bei sehr großen und/oder kleinen x-Werten wie eine lineare Funktion verhält, besitzt sie eine schräge Asymptote, nämlich die Geraden, die Funktionsgraph dieser linearen Funktion ist. Dies ist z. B. dann der Fall, wenn bei einer gebrochenrationalen Funktion der Grad des Zählerpolynoms genau um eins größer ist als der Grad des Nennerpolynoms.
Beispiel:
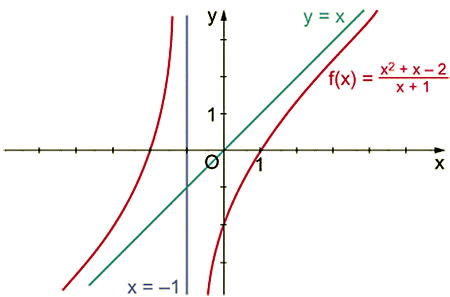
Für die gebrochenrationale Funktion \(f(x) = \dfrac{x^2 + x -2}{x + 1}\) ist \(\displaystyle \lim_{x\to\pm\infty}f(x) = \frac {x^2}{x} = x\), also hat sie die 1. Winkelhalbierende, d. h. die Gerade y = x, als schräge Asymptote. Auch in diesem Fall liegt bei x = –1 eine Polstelle udn damit eine senkrechte Asymptote vor.