Mit einem Funktionsgraphen kann man die Eigenschaften einer Funktion bildlich darstellen. Dazu werden jeder x-Wert und der dazugehörende Funktionswert (y-Wert, f(x)) als Koordinaten eines Punkts in der Ebene aufgefasst und mithilfe eines rechtwinkligen (kartesischen) Koordinatensystems aufgezeichnet. Bei der Darstellung von Funktionsgraphen nennt man das Koordinatensystem meist „Achsenkreuz“.
In der Schule sind die meisten behandelten Funktionen auf Intervallen von reellen Zahlen oder sogar auf ganz \(\mathbb R\) definiert. In diesem Fall ist der Graph eine „glatte“, d. h. stetige Kurve oder sogar eine Gerade.
Viele Eigenschaften von Funktionsgraphen wie Grenzwerte, Hoch- und Tiefpunkte, Asymptoten u. Ä. kann man bei einer Kurvendiskussion mit analytischen Mitteln berechnen.
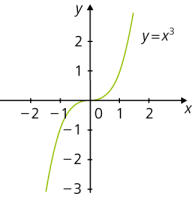
Beispiel:
Der Funktionsgraph der Funktion y = x3 ist eine kubische Parabel.