• Aufgabe 1

    6 Minuten 4 Punkte
    einfach

    Berechne die mittlere Änderungsrate von f(x)=3x-x² im Intervall [0;1].

  • Aufgabe 2

    12 Minuten 8 Punkte
    einfach

    Gib jeweils die Ableitungsfunktion an. Verwende im Ergebnis nur positive Exponenten.

       a) f(x)=-2x^{4}+2,5x^{2}-x+4

       b) g(x)=-\frac{4}{x²}+3

       c) h(x)=-\frac{1}{\sqrt{x}}

       d) i(x)=(1,5+x)(x-2)x

  • Aufgabe 3

    10 Minuten 6 Punkte
    einfach

    Bestimme jeweils zu der gegebenen Ableitungsfunktion den Term der ursprünglichen Funktion.

       a) f'(x)=x^{2}+3x+5

       b) g'(x)=2x^{3}-\frac{1}{x^{2}}

       c) h'(x)=\frac{3}{\sqrt{x}}

  • Aufgabe 4

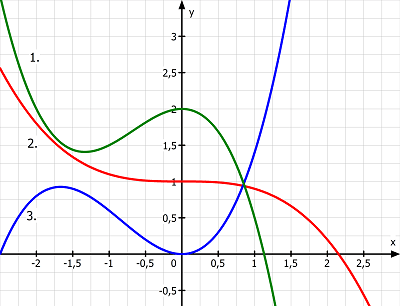
    9 Minuten 6 Punkte
    mittel

    Ordne jedem Funktionsgraphen seine Ableitungsfunktion zu.

    Funktionen

     

    Ableitungen

     

  • Aufgabe 5

    8 Minuten 6 Punkte
    mittel

    Die Parabel f(x)= \frac{1}{3}x²-\frac{1}{3} soll an der Stelle x = 2 ohne Knick in eine Gerade übergehen. Wie lautet die Gleichung dieser Geraden?