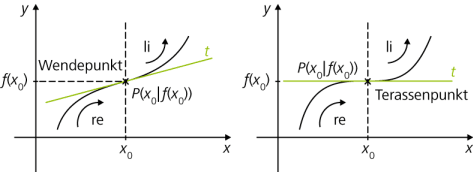
Ein Punkt P(x0|f(x0)) des Graphen Gf einer Funktion f heißt Wendepunkt (und die Stelle x0 dann eine Wendestelle), wenn sich dort die Krümmung des Graphen ändert. Die Tangente an diesem Punkt ist die Wendetangente. Ein Wendepunkt mit waagerechter Tangente ist ein Sattelpunkt bzw. Terrassenpunkt.
Bedingungen für Wendepunkte
Wenn eine zweimal differenzierbare Funktion f an der Stelle x0 einen Wendepunkt hat, dann ist ihre zweite Ableitung null (\(f'' ( x_0 ) = 0\)) und ihre Krümmung verschwindet dort. Umgekehrt muss die zweite Ableitung null sein, damit bei x0 ein Wendestelle sein kann – diese notwendige Bedingung ist aber nicht hinreichend, z. B. hat f(x) = x4 im Ursprung einen Tiefpunkt und keinen Wendepunkt, obwohl dort die zweite Ableitung null ist.
Eine hinreichende Bedingung für eine Wendestelle ist, dass die zweite Ableitung null wird und die dritte Ableitung an dieser Stelle ungleich null ist.
Eine andere hinreichende (und oft leichter zu überprüfende) Bedingung hierfür ist, dass die zweite Ableitung verschwindet und an dieser Stelle ihr Vorzeichen wechselt.