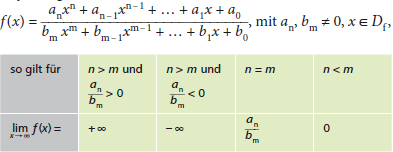Grenzwert von Funktionen

Der Grenzwert einer Funktion wird ähnlich definiert wie der Grenzwert einer Zahlenfolge, allerdings muss man zwei verschiedene Situationen unterscheiden (vgl. auch die Grenzwertsätze für Funktionen):

• Der Grenzwert an einer bestimmte Stelle (einem x-Wert) x₀. Dieser spielt einerseits eine Rolle bei der Definition und Untersuchung der Stetigkeit und Differenzierbarkeit einer Funktion, andererseits an Definitionslücken und Polstellen, an denen die Funktionswerte über alle Grenzen wachsen oder fallen.
• Der Grenzwert für \(x \rightarrow \pm \infty\), also wenn der x-Wert gegen plus oder minus unendlich strebt.

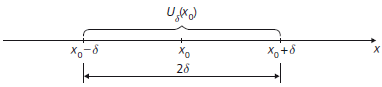
Beim Grenzverhalten einer Funktion f für \(x \rightarrow{x}_0\) untersucht man eine sog.  \(\delta\)-Umgebung von \(x_0\), dies ist das (kleine) offene Intervall \(U_\delta = \ ] x_0 - \delta ; x_0 + \delta [\), sowie die „punktierte \(\delta\)-Umgebung“ \(U_\delta \setminus \{x_0\}\).

Der Grenzwert \(\displaystyle \lim_{x\rightarrow x_0}f(x) = g\) existiert genau dann, wenn man für jedes (sehr kleine) \(\epsilon > 0\) eine (ebenfalls kleines)  \(\delta\)-Umgebung \(U_\delta\) von x₀ finden kann, sodass für alle \(x \in U_\delta\) gilt: \(|f(x) - g| < \epsilon\) (dies ist das sog. \(\epsilon\text -\delta\)-Kriterium).
Wenn dieser Grenzwert nur bei Annäherung von links (x < x₀) bzw. von rechts (x > x₀) existiert, nennt man ihn einen einseitigen (linksseitigen bzw. rechtsseitigen) Grenzwert und schreibt \(\displaystyle \lim_{x\rightarrow x_0 - 0}f(x)\) bzw. \(\displaystyle \lim_{x\rightarrow x_0 + 0}f(x)\).
Achtung: Wenn links- und rechtsseitiger Grenzwert einer Funktion an einer Stelle existieren, aber verschieden sind, existiert dort der Grenzwert dieser Funktion nicht!

Das Grenzverhalten einer Funktion „im Unendlichen“ untersucht man entweder mit Folgen von Funktionswerten. (f(x_n)), die für \(x \rightarrow \infty\) alle gegen denselben Grenzwert \(\displaystyle \lim_{x\rightarrow \infty}f(x) = g\) kovergieren müssen, oder wieder mit einem „Epsilon“: Wenn es für jedes \(\epsilon > 0\) eine Zahl s gibt, sodass für alle \(x \in D_f\) mit x > s gilt: \(| f (x) - g| < \epsilon\). f(x) nähert sich also beliebig dicht an den Grenzwert g an, wenn s nur groß genug gewählt wird.
Den Grenzwert für \(x \rightarrow -\infty\), also \(\displaystyle \lim_{x\rightarrow -\infty}f(x)\), definiert man ganz analog.
Die Gerade, an welche sich der Graph der Funktion für große bzw. kleine x anschmiegt, nennt man eine Asymptote des Graphen.

Beispiel:

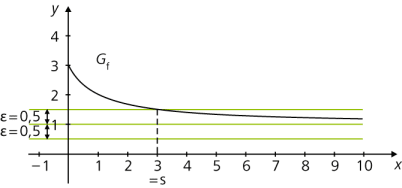
\(\displaystyle f (x) = \frac{x+3}{x+1} ,\ D_f = \mathbb{R}^+_0\) . Es gilt: \(\displaystyle \lim_{x \to \infty}\frac{x+3}{x+1} = 1\). Für x > 0  ist \(\displaystyle | f (x) - g| = \left| \frac{x+3}{x+1} -1 \right| = \frac{2}{x+1}\) . Also gilt \(\displaystyle \frac{2}{x+1} < \epsilon\ \Leftrightarrow \ x > \frac{2-\epsilon }{\epsilon }\) .
Für \(\epsilon = 0,5\) ist die Bedingung bereits erfüllt, wenn man \(\displaystyle s = \frac{2-\epsilon }{\epsilon } = 3\) wählt.

Wichtige Grenzwerte von Funktionen

• Ist eine gebrochenrationale Funktion gegeben mit
   
  

  

  
  Beispiele:
  \(\displaystyle \lim_{x \to \infty}\frac{3x^4+5}{7x^3-2x} = + \infty \),    \(\displaystyle \lim\limits_{x \to \infty}\frac{6x^5}{5x^5+8} = \frac{6}{5} \),    \(\displaystyle \lim\limits_{x \to \infty}\frac{-4x^3+50x^2}{10x^5} = 0\)
   
• Wurzelfunktionen
  \(\displaystyle \lim_{n \to \infty}\sqrt[n]{a}= 1 \ \ (a \in \mathbb{R}^+)\) 
  \(\displaystyle \lim_{n \to \infty}\sqrt[n]{n}= 1\)

• Potenzfunktionen, Exponential- und Logarithmusfunktionen, Fakultät
  Die Exponentialfunktion „wächst stärker“ als jede Potenzfunktion:   \(\displaystyle \lim_{x \to \infty}\frac{x^n}{e^x} = 0\) mit \(n \in \mathbb{N},\ x \in \mathbb{R}\)
  Die Logarithmusfunktion „wächst schwächer“ als jede Potenzfunktion:   \(\displaystyle \lim_{x \to \infty}\frac{\log x}{x^n} = 0\) mit \(n \in \mathbb{N},\ x \in \mathbb{R}^+\)
  Die Fakultät wächst stärker als jede Potenz aⁿ:  \(\displaystyle \lim_{n \to \infty}\frac{a^n}{n!} = 0\) für \(a \in \mathbb{R}\)
  Euler’sche Zahl:   ​\(\displaystyle \lim\limits_{n \to \infty} \left( 1 + \frac{1}{n} \right)^n = \text e = 2,718.28...\)
   
• Winkelfunktionen
  \(\displaystyle \lim_{x \to 0}\frac{\sin x}{x} = \lim_{x \to 0}\frac{\tan x}{x} = 1\) mit \(x \in \mathbb{R}\backslash\{0\}\) 
  \(\displaystyle \lim_{x \to 0}\frac{\sin ax}{x} = a\) mit \(a \in \mathbb{R}, x \in \mathbb{R}\backslash\{0\}\)
  \(\displaystyle \lim\limits_{x \to \infty}\frac{\sin(x)}{x}= 0\)