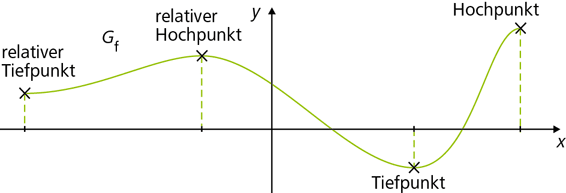
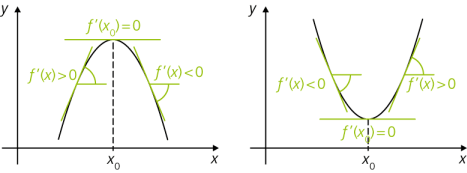An einer Extremstelle nimmt eine Funktion den größten bzw. kleinsten Wert in einer Umgebung U(x0) oder einem Intervall (lokales oder relatives Extremum) oder aber sogar auf dem gesamten Definitionsbereich Df (globales oder absolutes Extremum) an. (Statt Extremum kann man auch Extremwert sagen.)
Im Einzeln gilt:
-
Wenn für alle \(x \in U(x_0)\) gilt, dass \(f(x) \ge f(x_0)\), dann liegt an der Stelle x = x0 ein lokales (relatives) Minimum vor und der Punkt T(x0|f(x0)) ist ein lokaler (relativer) Tiefpunkt.
-
Wenn für alle \(x \in U(x_0)\) gilt, dass \(f(x) \le f(x_0)\), dann liegt an der Stelle x = x0 ein lokales (relatives) Maximum vor und der Punkt H(x0|f(x0)) ist ein lokaler (relativer) Hochpunkt.
-
Wenn für alle \(x \in D_f\) gilt, dass \(f(x) \ge f(x_0)\), dann liegt an der Stelle x = x0 ein globales (absolutes) Minimum vor und der Punkt T(x0|f(x0)) ist ein globaler (absoluter) Tiefpunkt.
-
Wenn für alle \(x \in D_f\) gilt, dass \(f(x) \le f(x_0)\), dann liegt an der Stelle x = x0 ein globales (absolutes) Maximum vor und der Punkt H(x0|f(x0)) ist ein globaler (absoluter) Hochpunkt.
Bedingungen für Extrema
Wenn eine differenzierbare Funktion f an der Stelle x0 ein Extremum hat, dann ist ihre erste Ableitung null (\(f' ( x_0 ) = 0\)) und sie hat eine waagerechte Tangente. Umgekehrt muss die Ableitung verschwinden, damit bei x0 ein Extremum sein kann – diese notwendige Bedingung ist aber nicht hinreichend, es kann bei einer waagerechten Tangente auch ein Sattelpunkt vorliegen (siehe unten).
Eine hinreichende Bedingung für ein Extremum ist, dass die erste Ableitung null wird und die zweite Ableitung an dieser Stelle ungleich null ist.
Eine andere hinreichende (und oft leichter zu überprüfende) Bedingung für ein Extremum ist, dass die erste Ableitung verschwindet und an dieser Stelle ihr Vorzeichen wechselt.
Dabei gilt (vgl. die obige Abbildung):
-
Wenn das Vorzeichen von \(f'\) von minus (Tangentensteigung negativ, fallender Funktionsgraph) auf plus (Tangentensteigung positiv, ansteigender Funktionsgraph) wechselt, dann liegt ein Tiefpunkt vor.
-
Wenn das Vorzeichen von \(f'\) von plus (Tangentensteigung positiv, ansteigender Funktionsgraph) auf minus (Tangentensteigung negativ, fallender Funktionsgraph) wechselt, dann liegt ein Hochpunkt vor.