Unter Parameterfunktionen versteht man in der Analysis Funktionen, in deren Funktionsterm außer der unabhängigen Variablen noch ein oder mehrere konstante Parameter auftreten. Variiert man solch einen Parameter, erhält man eine Menge von miteinander verwandten Funktionen, die man als Funktionenschar bezeichnet, ihre Graphen heißen zusammengenommen auch Kurvenschar.
Wenn alle Scharfunktionen lineare Funktionen sind, nennt man die Menge ihrer Graphen auch eine Geradenschar (die sich auch mit den Mitteln der Analytischen Geometrie untersuchen ließe).
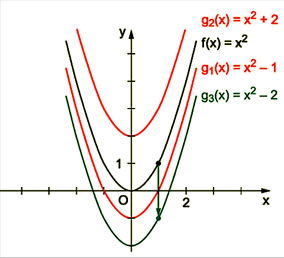
Beispiel:
Die Funktionenschar y = x2 + c besteht aus Parabeln, die entlang der y-Achse gegeneinander verschoben sind.
Bei der Kurvendiskussion von Parameterfunktionen soll oft eine sog. Ortskurve ermittelt werden. Dabei handelt es sich um die Menge aller Punkte, die bei verschiedenen Parameterwerten demselben Punkt auf dem jeweiligen Funktionsgraphen entsprechen. Im obigen Beispiel y = x2 + c ist die y-Achse die Ortskurve der Scheitelpunkte der Scharparabeln. Häufig ist auch die Ortskurve der Extrem- oder Wendepunkte in einer Funktionenschar gefragt.