Ein Kreis ist eine geometrische Kurve bzw. Figur, für die es zwei mögliche Definitionen gibt:
- Alle Punkte, die von einem gegebenen Punkt den gleichen Abstand haben, dieser Punkt ist der Mittelpunkt M des Kreises. Der konstante Abstand zum Mittelpunkt ist der Radius r des Kreises. So definiert ist ein Kreis eine gekrümmte, in sich geschlossene Linie bzw. Kurve.
- Alle Punkte, die von einem gegebenen Punkt höchsten einen bestimmten Abstand r haben, dieser Punkt ist der Mittelpunkt des Kreises. In diesem Fall ist der Kreis eine „gefüllte“ runde Fläche.
Um Missverständnissen vorzubeugen, sollte man im Zweifelsfall „Kreislinie“ zur Begrenzung des Kreises sagen und „Kreisfläche“, wenn die ganze Fläche, also alle Punkte zwsichen Mitte und Rand gemeint sind.
Der Umfang eines Kreises beträgt \(U = 2\pi r\), sein Flächeninhalt \(A = \pi r^2\). Dabei ist \(\pi \approx 3,14\ldots\) die sog. Kreiszahl.
Ein Kreis ist die symmetrischste Figur, die es gibt:
- Er ist drehsymmetrisch bei Drehung um jeden beliebigen Winkel.
- Er ist achsensymmetrisch bei Spiegelung an jeder Mittelpunktsgeraden, d. h. jeder Geraden, die durch den Mittelpunkt verläuft.
Wenn man zwei Punkte, die einander auf der Kreislinie exakt gegenüber liegen, verbindet, nennt man diese Strecke den Durchmesser d des Kreises, es ist d = 2r. Jeder Durchmesser ist eine Symmetrieachse.
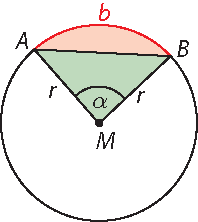
Eine Strecke \(\overline{AB}\), die zwei beliebige Punkte A und B auf der Kreislinie verbindet, aber nicht durch M geht, heißt Sehne. Der Teil der Kreislinie zwischen A und B ist der Kreisbogen \(\widehat{AB}\). Seine Länge b kann man bestimmen, wenn man den Mittelpunktswinkel \(\alpha\) im Bogenmaß angibt: \(\alpha = \displaystyle \frac b r \Rightarrow b = \alpha \cdot r\). Die rote Fläche in der Skizze nennt man ein (Kreis-)Segment, die rote und die grüne Fläche zusammen bilden einen Sektor des Kreises.
Eine Mittelpunktsgerade (Zentrale) läuft durch den Mittelpunkt eines Kreises. Sie ist ein Spezialfall einer Sekanten, also einer Geraden, die die Kreislinie in zwei Punkten schneidet. Eine Gerade, die mit einem Kreis genau einen Punkt gemeinsam hat, heißt Tangente, eine Passante hat keinen gemeinsamen Punkt mit dem Kreis.
In der Analysis kann man einen Kreis zwar nicht als Graph einer Funktion darstellen, weil dann fast zu allen x-Werten zwei Funktionswerte existieren würden. Es ist aber möglich, einen Halbkreis, genauer gesagt die „obere“ Hälfte eines Kreises im Achsenkreuz darzustellen. Wenn der Kreismittelpunkt im Ursprung liegt und der Radius 1 ist, bekommt man recht einfach mit dem Satz des Pythagoras eine implizite Form der Funktionsgleichung: y2 + x2 = 1. Durch Umformen erhält man daraus den (expliziten) Funktionsterm des Halbkreises \(\displaystyle y = f(x) = \sqrt {1 - x^2}\). Die Definitionsmenge ist Df = [–1; 1], die Wertemenge Wf = [0; 1].
In der Analytischen Geometrie werden Kreise genau wie Ebenen durch Gleichungen angegeben. Für einen Kreis k mit Mittelpunkt M(m1|m2) und Radius \(r\) gibt es die folgenden möglichen Gleichungen:
- Vektorform: \((\vec x - \vec m)^2 = r^2\)
- Koordinatenform: (x1 – m1)2 + (x2 – m2)2 = r2
- Parameterform: \(\vec x = \vec m + r \begin{pmatrix} \cos t \\ \sin t \end{pmatrix} \ \ (0 \le t < 2\pi)\)
Beispiel:
Kreis um den Mittelpunkt \(M(4|-3)\) mit dem Radius \(5\).
- In Vektorform \(\displaystyle \left( \vec x - \binom{4}{-3}\right)^2 = 5^2 .\)
- In Koordinatenform: \(( x_1 - 4)^2 + ( x_2 + 3)^2 = 5^2 .\)
- In Parameterform: \(\begin{cases} x_1 = 4 + 5 \cdot \cos t \\ x_2 = -3 + 5 \cdot \sin t \end{cases}(0 \leq t < 2\pi ).\)
Manche Rechnungen am Kreis vereinfachen sich, wenn sich nicht in kartesischen, sondern in Polarkoordinaten durchführt.