An einem Kreis kann man verschiedene Winkel betrachten:
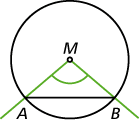
- Ist \(\overline{AB}\) eine Sehne des Kreises mit dem Mittelpunkt \(M\), dann heißt \(\measuredangle\) \(AMB\) Mittelpunktswinkel.
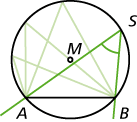
- Ist \(\overline{AB}\) eine Kreissehne und \(S\) ein Punkt auf dem Kreisumfang, dann heißt\(\measuredangle\) \(ASB\) Umfangswinkel.
Beachte: Zu einer gegebenen Sehne \(\overline{AB}\) gehören ein Mittelpunktswinkel, aber unendlich viele Umfangswinkel.
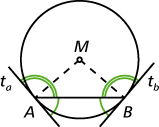
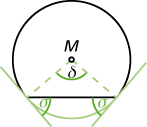
- Ist \(\overline{AB}\) eine Sehne und sind \(t_a, t_b\) Kreistangenten in \(A\) bzw. \(B,\) dann heißt der von der Sehne \(\overline{AB}\) und einer Tangente eingeschlossene Winkel Sehnentangentenwinkel.
Beachte: Sowohl in A als auch in B entstehen je zwei Sehnentangentenwinkel; sie ergänzen sich zu 180°.
Es gelten die folgenden Sätze:
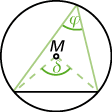
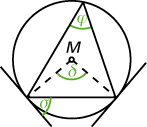
- Der Mittelpunktswinkel \(\delta\) ist doppelt so groß wie der auf der gleichen Seite der Sehne liegende Umfangswinkel \(\varphi\).
- Der Mittelpunktswinkel \(\delta\) ist auch doppelt so groß wie der zum gleichen Kreisgoben gehörenden Sehnentangentenwinkel \(\sigma\).
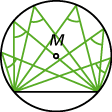
- Umfangswinkel auf dem gleichen Bogen sind gleich.
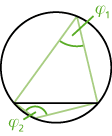
- Die Umfangswinkel \(\varphi_1\) und \(\varphi_2\) auf einem Bogen und dem Restbogen ergänzen sich zu 180°.
- Der Sehnentangentenwinkel \(\sigma\) und der zum gleichen Kreisgoben gehörende Umfangswinkel \(\varphi\) sind gleich groß.