Der Satz des Pythagoras ist einer der berühmtesten Sätze der Mathematik, wenn nicht aller Naturwissenschaften. Er besagt, dass in einem rechtwinkligen Dreieck der Flächeninhalt der beiden Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrats ist:
a2 +b2 = c2
Man fasst den Satz zusammen mit Kathetensatz, Höhensatz und verallgemeinertem Pythagoras-Satz auch zur sog. Satzgruppe des Pythagoras zusammen.
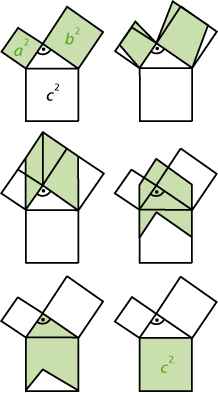
Es gibt unzählige Beweise für diesen Satz, eine Beweisidee illustriert die nachstehende Bilderfolge (man beachte, dass die Fläche eines Parallelogramms gleich bleibt, wenn man eine Seite parallelverschiebt).
Aus dem Satz des Pythagoras folgt, dass rechtwinklige Dreiecke bereits durch die Angabe von 2 Seiten bestimmt sind, die dritte Seite muss dem „Pythagoras“ gehorchen!
Beispiele:
- Die Katheten sollen die Längen \(5\) bzw. \(12\) haben. Die Hypotenuse \(h\) muss \(h^2 = 5^2 + 12^2\) erfüllen. \(h^2 = 16\)9 bedeutet: ihre Länge muss \(h = 13\) sein!
- Die Hypotenuse soll \(9\), eine Kathete \(7\) lang sein. Die andere Kathete \(k\) muss dann \(9^2 = 7^2 + k^2\) erfüllen. \(k^2 = 9^2 - 7^2 = 32\) bedeutet: \(k = \sqrt{32} \approx 5,66\).
Wenn drei verschiedene natürliche Zahlen die Bedingung des Pythagoras-Satzes erfüllen, nennt man sie „pythagoräische Tripel“. Einfache Beispiele sind (3; 4; 5), (5: 12; 13) (siehe oben) oder (20; 21; 29).
Die Umkehrung des Pythagoras-Satzes gilt ebenfalls: Wenn für die Seiten eines Dreiecks die Beziehung a2 +b2 = c2 gilt, dann ist das Dreieck rechtwinklig und hat die Hypotenuse c.
Der Satz des Pythagoras spielt auch in der Trigonometrie eine grundlegende Rolle, beispielsweise liegt er der wichtigen Beziehung sin2x + cos2x = 1 zugrunde.