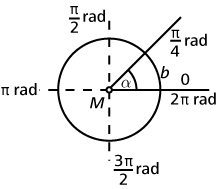
Das Bogenmaß ist ein Maß für die Größe eines Winkels. Und zwar ist das Bogenmaß eines Winkels das Verhältnis aus der Bogenlänge, also der Länge des Kreisbogens b, und dem Radius r des Kreises. Die Einheit ist m/m, also 1, man verwendet aber öfters die „Dummy-Einheit“ Radiant (rad), um deutlich zu machen, dass es gerade um einen Winkel geht:
\(\alpha [\text{rad]} = \displaystyle \frac{b}{r}\)
Man kann sich die Beziehung auch gut in der folgenden Form merken: \(\displaystyle \frac{\text{Kreisbogen}}{\text{Kreisumfang}} = \frac{\text{Mittelpunktswinkel}}{\text{Vollwinkel}}\)
Der gesamte Kreisumfang beträgt \(U = 2\pi r\), also ist ein Vollwinkel in Bogenmaß \(\displaystyle \frac{2\pi r}{r} = 2\pi\). Daraus erhält man die folgenden Umrechnungsformeln zwischen Bogenmaß und Gradmaß (Altgrad):
\(\displaystyle \alpha [\text{rad}] = \frac{\alpha [°] }{360^{\circ} } \cdot 2\pi\)
\(\displaystyle \alpha [°] = \frac{\alpha [\text{rad}]}{2\pi } \cdot 360^{\circ}\)
Wichtige Werte:
Am Taschenrechner kann man Winkel in Gradmaß (Taste DEG) und Bogenmaß (RAD) angeben lassen.