Geraden gehören zu den grundlegenden Objekten der Geometrie, es handelt sich dabei um im Alltagssinn „gerade“ Linien, die sich ohne Anfangs- und Endpunkt bis ins Unendliche erstrecken. Geraden sind Punktmengen, bei denen zwischen zwei Punkten immer noch unendlich viele weitere Punkte liegen – so wie bei der reellen Zahlengeraden, die tatsächlich auch eine Gerade im geometrischen Sinn ist.
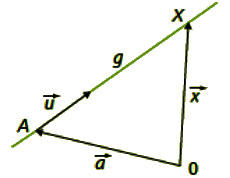
Eine Gerade g wird entweder durch zwei Punkte A und B eindeutig festgelegt oder durch einen Punkt A bzw. dessen Ortsvektor \(\vec a\) und einen Richtungsvektor \(\vec u\) (siehe unten), der angibt, „wohin“ die Reise ins Unendliche führt.
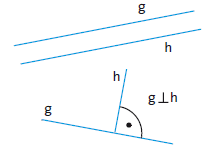
Parallele Geraden haben keinen Punkt gemeinsam oder sie sind identisch. Senkrechte Geraden schneiden sich unter einem rechten Winkel.
Wenn sich zwei Geraden in der Ebene (im Zweidimensionalen) schneiden, haben sie genau einen Punkt gemeinsam. Im (dreidimensionalen) Raum können Geraden auch windschief zueinander stehen, also weder parallel sein noch einen Schnittpunkt haben.
Eine Gerade wird durch einen Punkt in zwei Halbgeraden (Strahlen) zerlegt.
In der Analytischen Geometrie kann man Geraden mithilfe von Gleichungen charakterisieren. Man unterscheidet dabei zwischen Geradengleichungen in Parameterform (Punkt-Richtungs-Form, \(g\!: \vec x = \vec a + \lambda \cdot \vec u\), oder Zweipunkteform, \(g\!: \vec x = \vec a + \lambda \cdot \left( \vec b - \vec a \right)\)) und Koordinatenform. Eng verwandt mit der Koordinatenform ist die Normalform.
Ein wichtiges Untersuchungsgebiet in der Anlalytischen Geometrie sind Abstände und Lagebeziehungen von Geraden, Ebenen und Punkten.