Winkel und Kreise (2)

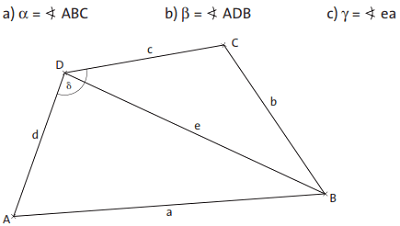
Trage in der Abbildung die angegebenen Winkel ein.

Bezeichne in der Abbildung aus Aufgabe 2 den Winkel \(\delta\) mithilfe von …

1. Strecken: \(\delta\)=                           
2. Punkten: \(\delta\) =                           

Bestimme bei den Winkeln \(\alpha,\beta,\gamma\) und \(\delta\) aus den Aufgaben 2 und 3 die Winkelart.
\(\alpha\) =                       
\(\beta\) =                       
\(\gamma\) =                       
\(\delta\) =                       

Wolfgang hat ein rechteckiges Gartengrundstück mit den Seitenlängen 40 m und 30 m. Er stellt genau in der Mitte seines Grundstücks einen Rasensprenger auf, der eine kreisrunde Fläche beregnet.

1. Wie weit muss der Strahl spritzen, damit wirklich das gesamte Grundstück bewässert wird? Konstruiere.
2. Wie weit muss Wolfgang den Strahl einstellen, damit dieser nicht über die Grundstücksgrenze hinweg spritzt?
3. Wie groß ist dann die Fläche, die nicht beregnet wird? 

Beantworte folgende Fragen. (Tipp: Eine Skizze hilft dir. Du sollst die Aufgaben jedoch durch Rechnung lösen, nicht durch Konstruktion.)

1. Wie groß ist der Winkel, den der Minutenzeiger einer Uhr in der Zeit von 9.45 Uhr bis 10.10 Uhr überstreicht? 
2.  In welcher Zeit dreht sich der Stundenzeiger einer Uhr um 120°?
3. Wie groß ist der kleinere der beiden Winkel, die der Stunden- und der Minutenzeiger um 20 Uhr bilden? Wie groß ist dann der größere Winkel?
4. Bezeichne den kleineren Winkel aus c) mithilfe der Abkürzungen s für den Stunden- und m für den Minutenzeiger.
5. Wie viel Uhr ist es, wenn der Minutenzeiger m auf die 12 zeigt und es gilt  sm = 300°?
6. Der große Zeiger hat sich um 420° gedreht. Wie viel Zeit ist vergangen?