Ganzrationale Funktionen

Ganzrationale Funktionen oder Polynomfunktionen sind Funktionen, deren Funktionsterm ein Polynom  ist, also \(f(x) = a_nx^n + a_{n-1}x^{n-1} + \ldots + a_1x + a_0\). Ihre maximale Definitionsmenge ist \(D_f = \mathbb R \setminus \{x| v(x) = 0\}\). Wie bei Polynomen nennt man die höchste auftretende Potenz von x den Grad f der ganzrationalen Funktion. Funktionen, die sich als der Quotient von zwei Polynomen schreiben lassen, nennt man gebrochenrationale Funktionen, für ganz- und gebrochenrationale Funktionen zusammen gibt es den Oberbegriff „rationale Funktion“.

Beispiele:

• Grad f = 0: konstante Funktion \(f\! : \ x \mapsto a, a \in \mathbb{R}\)

• Grad f = 1: lineare Funktion \(f\! : \ x \mapsto mx + b \ \ (m,b \in \mathbb R)\)

• Grad f = 2: quadratische Funktion \(\displaystyle f\! : \ x \mapsto 3 x^2 + \frac 1 2 x - 15\)

• Grad f = 5: \(f\! : \ x \mapsto - 2 x^5 + 4 x^2 + 5x\)

Eigenschaften

• Wenn in einer ganzrationalen Funktion alle Potenzen gerade sind (z. B. f(x) = –12x² + 4x⁴ + 1), ist ihr Graph spiegelsymmetrisch zur y-Achse und sie ist eine gerade Funktion. Sind alle Potenzen ungerade (z. B. f(x) = x¹¹ - 4x), dann ist der Graph punktsymmetrisch zum Ursprung und die Funktion ist ungerade.

• Gerade ganzrationale Funktionen sind – je nach Vorzeichen des Koeffizienten der höchsten Potenz – entweder nach oben oder nach unten beschränkt. Ungerade ganzrationale Funktionen sind immer unbeschränkt.
  Beispiele:
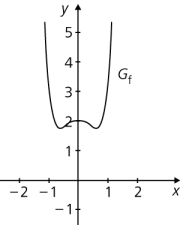
  Die gerade Funktion \(f : x \mapsto 2 x^6 - x^2 + 1\) ist nach unten beschränkt, z. B. ist Null eine untere Schranke. Der Grenzwert der Funktion ist \(\lim\limits_{x \to \infty }f (x) = \lim\limits_{x \to -\infty }f (x) = +\infty\).
  

  

  
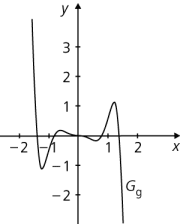
  Die ungerade Funktion \(g : x \mapsto - 1,5 x^7 + 4 x^5 - 2 x^3\) ist unbeschränkt. Es gilt: \(\lim\limits_{x \to -\infty }g (x) = +\infty\) und \(\lim\limits_{x \to +\infty }g (x) = -\infty\).
  

  

• Die Nullstellen sind die Lösungen der Polynomgleichung \(a_nx^n + a_{n-1}x^{n-1} + \ldots + a_1x + a_0 = 0\). Eine ganzrationale Funktion n-ten Grades hat höchstens n Nullstellen.
  Die ganzrationale Funktion f(x) hat genau dann bei x = x₀ eine Nullstelle, wenn sie als Polynom durch (x – x₀) dividiert werden kann.
  Daher ist die Standardtechnik bei ganzrationalen Funktionen höheren Grades, so viele Nullstellen zu raten, dass man sie durch Polynomdivision auf eine quadratische Funktion reduzieren kann, deren Nullstellen z. B. mit der Mitternachtsformel bestimmt werden können.
  Wenn man einen Faktor mehrfach (k-mal) ausklammern kann, nennt man die zugehörige Nullstelle eine k-fache Nullstelle.
  Beispiel:
  Für \(f : x \mapsto x^3 + x^2 - 5x + 3 \ (x \in \mathbb{R})\)kann man die Nullstelle x₀ = 1 durch Ausprobieren bzw. Einsetzen erraten. Polynomdivision ergibt \(( x^3 + x^2 - 5x + 3) : (x - 1) = x^2 + 2x - 3\). Für den quadratischen Faktor berechnet man die Nullstellen x = –1 ± 2, also x = –3 und x = 1. Damit ist x = 1 eine doppelte Nullstelle und x = –3 eine einfache Nullstelle.