Eine Funktion, Zahlenfolge oder Reihe heißt beschränkt, wenn es einen Wert gibt, der größer oder kleiner als alle Funktionswerte bzw. Glieder der Folge oder Reihe ist (da man Folgen und Reihen auch als Funktionen mit Definitionsmenge \(D = \mathbb N\) auffassen kann, wird im Folgenden nur von Funktionen die Rede sein). Formaler sagt man:
-
Eine Funktion \(f\!: D_f \rightarrow W_f, \ x \mapsto f(x)\) heißt nach unten beschränkt, wenn es eine Zahl \(s \in \mathbb R\) gibt, sodass \(f(x) \ge s\) für alle \(x \in D\) ist. s nennt man dann eine untere Schranke von f.
-
Eine Funktion \(f\!: D_f \rightarrow W_f, \ x \mapsto f(x)\) heißt nach oben beschränkt, wenn es eine Zahl \(s \in \mathbb R\) gibt, sodass \(f(x) \le s\) für alle \(x \in D\) ist. s nennt man dann eine obere Schranke von f.
Wenn s eine untere Schranke von f ist, liegen alle Punkte des Funktionsgraphen Gf oberhalb oder auf der Parallelen zur x-Achse mit der Gleichung y = s, entsprechend liegt bei einer oberen Schranke S der komplette unterhalb oder auf der Geraden y = S.
Beispiel:
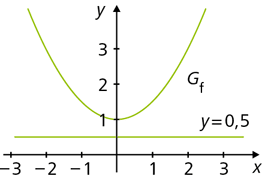
Die quadratische Funktion \(f:x \mapsto 0,5x^2+1 \ (\ x\in \mathbb{R})\) ist nach unten beschränkt, da z. B. gilt: \(0,5x^2+1\geq 0,5\) für alle \(x \in \mathbb{R}\). s = 0,5 ist hier also eine untere Schranke.
Beachte: Wenn eine Zahl s eine untere (obere) Schranke für eine Funktion ist, sind alle kleineren (größeren) Zahlen natürlich erst recht untere (obere) Schranken. Es gibt also immer unendlich viele Schranken – oder keine, wenn eine Funktion unbeschränkt ist.
Die größte untere Schranke einer Funktion nennt man das Infimum und schreibt dafür inf f. Die kleinste obere Schranke ist das Supremum sup f.
Wenn eine Funktion sowohl nach unten als auch nach oben beschränkt ist, heißt sie beschränkt. Es gibt dann also mindestens eine Zahl \(r \in \mathbb{R}^+\), für die gilt: \(|f(x)|\leq r\) für alle \(x\in D\). Ein bekanntes Beispiel für (beidseitig) beschränkte Funktionen sind die Winkelfunktionen Sinus und Kosinus, beiden jeweils inf f = –1 und sup f = +1 ist.