Eine lineare Funktion ist in der Analysis eine Funktion, deren Funktionsterm die Form y = f(x) = mx + b hat, auf ganz \(\mathbb R\) definiert ist und deren Werte in ganz \(\mathbb R\) liegen. Für ihre Definitions- und Wertemenge gilt also \(D_f = W_f = \mathbb R\), es sei denn, man hat den (ziemlich langweiligen) Fall m = 0: Dann ist \(D_f = \mathbb R\) und Wf = {b}.
Wenn b = 0 ist, nennt man die lineare Funktion eine proportionale Funktion, die man auch proportionale Zuordnung nennt. Der Funktionsterm lautet dann einfach f(x) = mx und die Steigung m entspricht dem Proportionalitätsfaktor.
Der Graph einer linearen Funktion ist eine Gerade.
Die Konstante (der Parameter) m nennt man die Steigung. b ist der y-Achsenabschnitt, denn es ist f(0) = m · 0 + b = b. Wenn die Steigung positiv ist, steigt der Graph streng monoton an, bei negativem m fällt er streng monoton, bei m = 0 ist der Graph waagerecht (parallel zur x-Achse).
Im rechtwinkligen Steigungsdreieck mit der horizontalen Kathete der Länge 1 hat die vertikale Kathete die Länge \(|m|\). Daher gilt für den Neigungswinkel \(\alpha\) (also dem Winkel zwischen der x-Achse und der Geraden):
\(\displaystyle m = \tan \alpha = \dfrac {f ( x_2 ) - f ( x_1 )} {x_2 - x_1} \ \ ( x_1 \neq x_ 2 )\)
Diese Beziehung spielt bei der Definition der Ableitung eine wichtige Rolle.
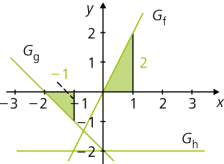
Beispiele
-
\(f : x \mapsto 2 x, m = 2; t = 0\)
-
\(g : x \mapsto - x - 2, m = - 1; t = - 2\)
-
\(h : x \mapsto - 2, m = 0; t = - 2\)
Man kann aus den Steigungen zweier Geraden ihren Schnittwinkel ausrechnen (Lagebeziehungen von Funktionsgraphen). Sind ein Punkt und die Steigung oder zwei Punkte gegeben, lassen sich daraus die übrigen Parameter berechnen (analytische Bestimmung von Geradengleichungen).
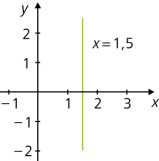
Achtung: Eine vertikale (senkrechte), also zur y-Achse parallele Gerade kann kein Graph einer Funktion sein, weil es dann zu einem Funktionswert nicht nur mehr als einen,sondern sogar unendlich viele Funktionswerte gäbe! Man kann sie aber natürlich trotzdem durch eine Gleichung beschreiben (z. B. x = 1,5) und im Koordinatensystem darstellen. Vertikale Geraden treten oft als Asymptoten von Funktionen auf wie y = tan x oder y = 1/x.