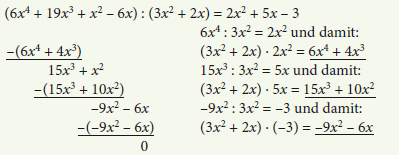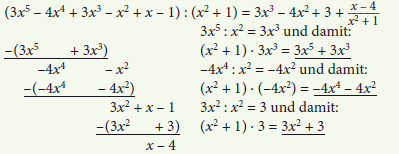Die Polynomdivision ist ein Rechenverfahren bzw. eine Termumformung, bei der ein Bruchterm, genauer gesagt der Quotient aus zwei Polynomen in eine Summe aus zwei Termen umgeformt wird, und zwar einem einfacheren Polynom und ggf. einem einfacheren Bruchterm:
\(\dfrac{Z(x)}{N(x)} = Z(x) : N(x) = Q(x) \ \left[+ \dfrac{r(x)}{N(x)} \right]\)
Dabei sind Z(x) das Zähler und N(x) das Nennerpolynom bzw. Dividend und Divisor, Q(x) das „Ergebnis“ (der Quotient) und r(x) das Restpolynom. Diese Bezeichnung kommt daher, dass man auch schreiben kann:
\(Z(x) = Q(x) \cdot N(x) \ \left[+ r(x)\right]\)
Man geht dabei ähnlich vor wie beim schriftlichen Dividieren von Zahlen: Nach und nach werden Vielfache des Divisors vom Dividenden subtrahiert. Die Summanden des Quotienten erhält man schrittweise durch Division des jeweils noch vorhandenen „vordersten“ Gliedes des Dividenden durch das erste Glied des Divisors.
Beispiele:
Achtung: In beiden Polynomen (Dividend und Divisor) müssen die Summanden vor der Division nach ihrem Grad, also nach den Exponenten von x, in absteigender Reihenfolge geordnet sein.
Anwendungen für die Polynomdivision gibt es z. B.
- bei der Kurvendiskussion von gebrochenrationalen Funktionen,
- bei der Partialbruchzerlegung und
- beim Lösen von Polynomgleichungen höheren Grades bzw. bei der Bestimmung von Nullstellen von Polynomfunktionen – man „rät“ eine Nullstelle x0 und teilt dann das Polynom durch (x – x0), was auf ein Polynom mit einem um 1 niedrigeren Grad führt.