Periodische Funktionen

Eine Funktion $f\!: x \mapsto f(x) \ \ (x\in D_f)$ heißt periodisch, wenn es eine von 0 verschiedene Zahl p gibt, sodass für alle $x\in D_f$ gilt:

Mit x ist auch x + p in D_f und es ist f(x + p) = f(x).

p ist dann die Periode dieser Funktion.

Beachte: Wenn es eine Periode p gibt, dann hat die entsprechende Funktion gleich unendliche viele Perioden, denn jede Zahl k · p mit $k \in \mathbb{Z}$  erfüllt die Periodizitätsbedingung genauso. Jede periodische Funktion besitzt somit unendlich viele Perioden. Meist gibt man zu einer Funktion ihre kleinste positive Periode an. 

Beispiel:
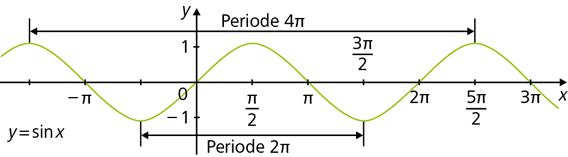
$f:x \mapsto \sin x, \ x\in \mathbb{R}$ ist periodisch mit der Periode $p=2\pi$, denn es ist $\sin(x+2\pi)=\sin x$ für alle $x\in \mathbb{R}$. 

$4\pi$ ist ebenfalls eine Periode von f: $\sin (x+4\pi) = \sin x$.