Polstellen

Eine Polstelle (auch: ein Pol, eine Unendlichkeitsstelle) ist ein x-Wert, bei dem der Graph einer Funktion eine senkrechte (vertikale) Asymptote hat, also der Funktionswert gegen\(\pm\infty\) divergiert. An dieser Stelle ist die Funktion daher nicht definiert, weswegen man auch von einer Definitionslücke spricht. Allerdings gibt es auch sog. hebbare Definitionslücken, die sich stetig schließen lassen (siehe unten).

Polstellen können vor allem bei gebrochenrationalen Funktionen von der Form \(\displaystyle f(x) = \frac{Z(x)}{N(x)}\) auftreten, und zwar dann, wenn für ein bestimmtes x = x₀ das Nennerpolynom N(x) eine Nullstelle hat. Nun muss man unterscheiden:

• Das Zählerpolynom Z(x) hat bei x₀keine Nullstelle. Dann ist eine k-fache Nullstelle des Nennerpolynoms eine k-fache Polstelle; bei ungeradem k (also insbesondere bein einer einfachen Nullstelle) findet ein Vorzeichenwechsel statt, bei geradem k nicht.
  Beispiele:
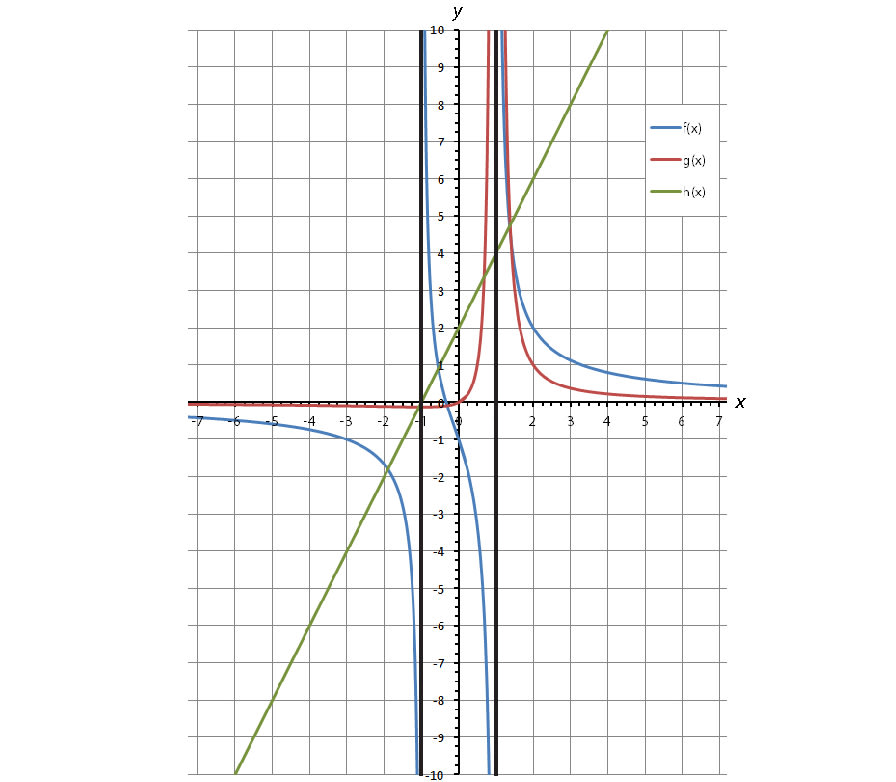
  \(\displaystyle f(x) = \frac{3x+1}{x^2-1} = \frac{3x+1}{(x-1)(x+1)}\), N(x) hat zwei einfache Nullstellen bei x_0;1 = –1 und x_0;2 = +1, also zwei („ungerade“) Polstellen mit Vorzeichenwechsel.
  \(\displaystyle g(x) = \frac{0,5x}{x^2-2x+1} = \frac{0,5x}{(x-1)^2}\), N(x) hat eine doppelte Nullstelle x₀ = +1, also eine doppelte („gerade“) Polstelle ohne Vorzeichenwechsel.
• Das Zählerpolynom Z(x) hat bei x₀ eine j-fache Nullstelle. Wenn j < k ist, kürzen sich die Zählernullstellen gegen die Nennernullstellen weg und es bleibt wiederum eine Polstelle übrig. Wenn dagegen \(j \ge k\)  ist, kürzen sich die Nenner-Nullstellen weg und die Funktion kann an x₀ stetig fortgesetzt werden.
  Beispiel:
  \(\displaystyle h(x) = \frac{2x^2-2}{x-1} = \frac{2(x-1)(x+1)}{(x-1)}\), N(x) hat eine einfache Nullstelle bei x₀ = +1, die aber ebenso eine Nullstelle des Zähler ist. Es ist daher in ganz D_f h(x) = 2(x + 1) und die „Lücke“ im Definitionsbereich kann durch h(1) = 4 geschlossen bzw. gehoben werden.