Wurzelfunktionen kann man auf zwei äuqivalente Weisen definieren:
-
Sie sind Potenzfunktionen mit einem Stammbruch im Exponenten, haben also die Form
\(f\!: x \mapsto f(x) = x^{1/n} = \sqrt[n]{x} \ \ (x \in \mathbb R_0^+, \ n \in \mathbb N)\). -
Sie sind die Umkehrfunktionen der Potenzfunktionen mit natürlichen Exponenten, sofern man diese auf den Definitionsbereich auf \(D_f = \mathbb R_0^+\) einschränkt:
\(x = f(y) = y^n \ \ \Rightarrow \ \ y = g(x) = x^{1/n} = \sqrt[n]{x} \ \ (x \in \mathbb R_0^+, \ n \in \mathbb N) \) bzw. g = f–1 und f = g–1
Außerdem kann man natürlich auch eine Wurzelfunktion als eine Potenzfunktion mit rationalem Exponenten ansehen, deren Exponent den Nenner 1 hat.
Manchmal ist mit „Wurzelfunktion“ speziell die Quadratwurzelfunktion, also der Fall n = 2 gemeint. Sie ist die Umkehrfunktion der quadratischen Funktion y = x2, deren Funktionsgraph die Normalparabel ist. Man lässt dann den Wurzelexponenten n weg, schreibt also einfach \(y = \sqrt x\). Im Zweifelsfall sollte man immer angeben (oder nachfragen) ob es gerade um die Quadratwurzel oder um eine allgemeinere Wurzelfunktion geht.
Der Funktionsgraph aller Wurzelfunktionen ist streng monoton steigend. Daher ist der Ursprung als linker Rand des Definitionsbereichs das (einzige) globale Minimum.
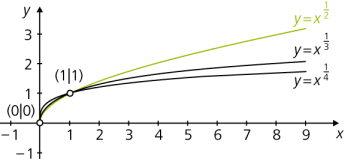
Außer dem Ursprung (0|0) haben alle Graphen auch den Punkt (1|1) gemein.
Da der Übergang zur Umkehrfunktion eine Spiegelung des Funktionsgraphen an der ersten Winkelhalbierenden bedeutet, sind die Graphen der Wurzelfunktionen „liegende“ Parabeläste.
Beispiele:
-
\(y = x^\frac{1}{2}\) ,
-
\(y = x^\frac{1}{3}\) ,
-
\(y = x^\frac{1}{4}\) ,