Im Allgemeinen ist eine Winkelhalbierende eine Gerade durch den Scheitel eines Winkels, welche das Winkelfeld in zwei gleich große Hälften teilt. Die Aufgabe, zu einem gegebenen Winkel die Winkelhalbierende nur mit Zirkel und Lineal zu finden, ist eine der sog. geometrischen Grundkonstruktionen.
In einem zweidimensionalen kartesischen Koordinatensystem (Achsenkreuz) nennt man die Geraden y = x und y = –x die erste bzw. zweite Winkelhalbierende, da sie den Winkel zwischen x- und y-Achse halbieren.
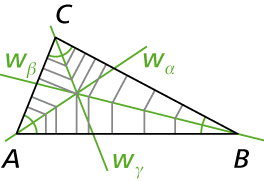
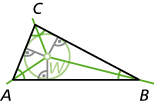
In einem Dreieck gehören die drei Winkelhalbierenden \(w_\alpha\), \(w_\beta\) und \(w_\gamma\) zu den besonderen Linien. Sie schneiden sich in einem gemeinsam Punkt W, der gleichzeitig der Mittelpunkt des Inkreises ist. Dies liegt daran, dass jeder Punkt auf einer Winkelhalbierenden zu den beiden Schenkeln gleiche Abstände hat, weswegen der Schnittpunkt W von allen drei Schenken den gleichen Abstand hat.
Deswegen kann man einen Kreis zeichnen, dessen Radius gerade dieser gleiche Abstand ist und alle drei Dreiecksseiten berührt – genau so ist der Inkreis definiert.
Der Umkreismittelpunkt eines Dreiecks ist der Schnittpunkt der Mittelsenkrechten.