Im Dreieck werden bestimmte Linien, die in einem besonderen Verhältnis zu den Seiten und/oder Winkeln stehen, als besondere Linien bezeichnet. Von jeder Art dieser besonderen Linien gibt es drei. Oft spielen auch die Schnittpunkte dieser jeweils drei Linien eine besondere Rolle. Im gleichschenkligen Dreieck sind jeweils zwei Linien zueinander spiegelsymmetrisch (nämlich die zu den gleich langen Schenkeln bzw. den Basiswinkeln gehörenden). Im gleichseitigen Dreieck fallen jeweils alle Arten von besonderen Linien zusammen.
Im einzelnen betrachtet man:
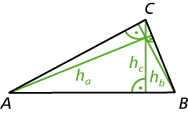
- Die Höhen ha, hb und hc eines Dreiecks sind die Senkrechten oder Lote von einem Eckpunkt auf die gegenüberliegende Seite.
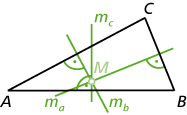
- Die Mittelsenkrechten oder Mittellote sind die Geraden, die senkrecht auf den Seitenmitten stehen. Man bezeichnet sie mit ma, mb und mc. Ihr Schnittpunkt ist der Umkreismittelpunkt M (siehe unten).
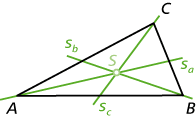
- Die Seitenhalbierenden sa, sb und sc sind Geraden, die jeweils durch eine Seitenmitte und den gegenüberliegenden Eckpunkt verlaufen. Ihr Schnittpunkt ist der Schwerpunkt S.
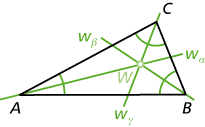
- Die Winkelhalbierenden sind Geraden; sie halbieren jeweils einen der Innenwinkel. Man bezeichnet siemit \(w_\alpha\), \(w_\beta\) und \(w_\gamma\). Ihr Schnittpunkt ist der Inkreismittelpunkt W.
Der Inkreis eines Dreiecks ist jener Kreis, der alle Dreiecksseiten berührt. Der Umkreis ist der Kreis, der durch die drei Eckpunkte des Dreiecks verläuft, sein Mittelpunkt ist M: