In der Geometrie versteht man unter den Grundkonstruktionen die im Folgenden dargestellten Aufgaben, wobei es immer darauf ankommt, nur mit Zirkel und Lineal zu arbeiten – und das Lineal darf nur zum Zeichnen, nicht zum Messen verwendet werden!
Eine andere häufige auftretende Konstruktionsaufgabe besteht darin, ein Dreieck aus drei sog. Hauptgrößen (Seitenlängen und Winkel) zu konstruieren, ebenfalls nur mit Zirkel und Lineal. Dies wird aber meist nicht zu den Grundkonstruktionen gezählt.
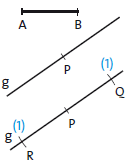
1. Abtragen einer Strecke
(1) Kreisbogen um \(P\) mit \(r = \overline{AB}\) zeichnen \(\Rightarrow\) Punkte \(Q\) und \(R\) auf \(g\)
Die Strecken \(PQ\) und \(PR\) auf \(g\) haben die gleiche Länge wie \(AB\).
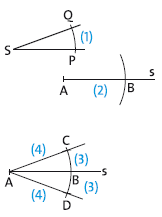
2. Antragen eines Winkels an einen Strahl
(1) Kreisbogen um \(S\) zeichnen \(\Rightarrow\) Punkte \(P\) und \(Q\)
(2) Kreisbogen um \(A\) mit Radius \(r = \overline{SP}\) zeichnen \(\Rightarrow\) Punkt \(B\) auf dem Strahl \(s\)
(3) Kreisbogen um \(B\) mit \(r = \overline{PQ}\) zeichnen \(\Rightarrow\) Punkte \(C\) und \(D\)
(4) Strahlen \(AD\) und \(AC\) zeichnen. Es gilt:
\(\measuredangle{BAD} = \measuredangle{CAB} = \measuredangle{QSP}\).
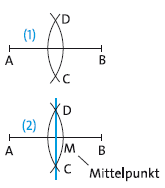
3. Strecke halbieren - die Mittelsenkrechte
(1) Kreisbogen um \(A\) und \(B\) zeichnen; Radius beliebig, gleich groß und \(r > \frac{1}{2}\overline{AB}\) ⇒ Punkte \(C\) und \(D\)
(2) Die Gerade \(CD\) schneidet die Strecke \(AB\) in \(\textbf{M}\). Sie ist die Mittelsenkrechte der Strecke \(AB\).
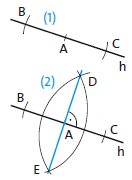
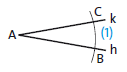
(1) Kreisbogen um den Scheitelpunkt \(A\) zeichnen \(\Rightarrow\) Punkt \(B\) auf \(h\) und Punkt \(C\) auf \(k\)
(2) Zwei Kreisbögen um \(B\) und \(C\) zeichnen, \(r>\frac{1}{2}\overline{BC}\Rightarrow\) Punkte \(D\) und \(E\) als Schnittpunkte der beiden Kreisbögen
\(AD\) ist die Winkelhalbierende von \(\measuredangle{(h, k)}\).
5. Senkrechte zu einer Geraden
(1) Kreisbogen um \(A\) zeichnen \(\Rightarrow B\) und \(C\) auf \(h\)
(2) Kreisbogen um \(B\) und \(C\) zeichnen; Radius beliebig, aber gleich groß, \(r>\overline{AB}\Rightarrow\) Punkte \(D\) und \(E\)
Die Gerade durch \(A, D, E\) ist die Senkrechte zu \(h\) in \(A\).
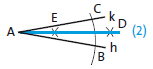
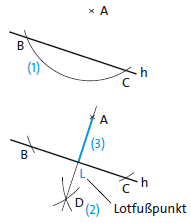
6. Lot von einem Punkt auf eine Gerade
(1) Kreisbogen um \(A\) zeichnen \(\Rightarrow B\) und \(C\) auf \(h\)
(2) Kreisbogen um \(B\) und \(C\) zeichnen; \(r>\frac{1}{2}\overline{BC}\) aber gleich groß \(\Rightarrow\) Punkt \(D\)
(3) Gerade durch \(A\) und \(D\) zeichnen \(\Rightarrow\) Punkt \(L\) auf \(h\)
\(AL\) ist das Lot von \(A\) auf die Gerade \(h\).