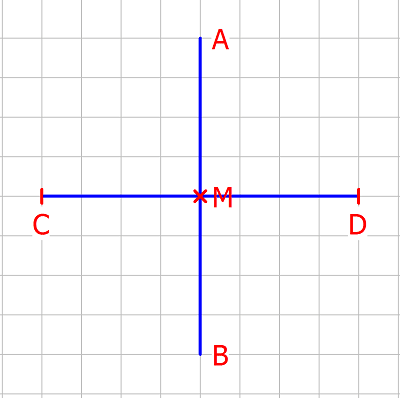
Die Mittelsenkrechte ist allgemein eine Gerade, die erstens senkrecht auf einer Strecke steht und zweitens diese Strecke genau in der Mitte schneidet.
Beispiel:
Die Gerade durch die Punkte A und B schneidet die Strecke \(\overline {CD}\) in dem Punkt M, der von den Punkten C und D denselben Abstand hat (also tatsächlich in der Mitte liegt).
Die Aufgabe, zu einer gegebenen Strecke die Mittelsenkrechte nur mit Zirkel und Lineal zu finden, ist eine der sog. geometrischen Grundkonstruktionen.
Eine besondere Rolle spielen die Mittelsenkrechten im Dreieck, da ihr Schnittpunkt der Mittelpunkt des Umkreises des Dreiecks ist.