Mittelsenkrechte und Umkreis im Dreieck

Allgemein ist die Mittelsenkrechte eine Gerade, die so auf einer Strecke senkrecht steht, dass sie diese genau in zwei gleich lange Hälften teilt.

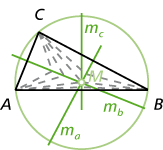
Im Dreieck gehören die Mittelsenkrechten m_a, m_b und m_c auf den Seiten a, b und c zu den besonderen Linien.

Sie schneiden sich alle in einem Punkt M, der gleichzeitig der Mittelpunkt des Umkreises des Dreiecks ist. Dies liegt daran, dass jeder Punkt auf m_a gleich weit von B und C und jeder Punkt auf m_b gleich weit von A und C entfernt ist. Darum ist der Schnittpunkt von m_a und m_b von allen drei Ecken gleich weit entfernt und damit insbesondere auch gleich weit von A und B – damit muss er definitionsgemäß auch auf der Mittelsenkrechten m_c liegen. Und weil der Schnittpunkt der Mittelsenkrechten den gleichen Abstand von allen Ecken hat, kann man einen Kreis mit diesem Abstand als Radius um ihn zeichnen, auf dessen Kreislinie alle drei Ecken liegen. Genau so ist aber der Umkreis definiert.

Beim spitzwinkligen Dreieck liegt der Umkreismittelpunkt innerhalb, beim stumpfwinkligen außerhalb des Dreiecks. Beim rechtwinkligen Dreieck liegt er auf der Hypotenuse und halbiert sie. Die Umkehrung dieser Aussage ist der Satz des Thales.

Der Inkreismittelpunkt eines Dreiecks ist der Schnittpunkt der Winkelhalbierenden.