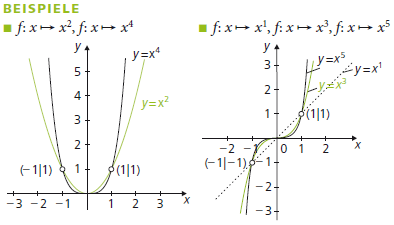Eine Potenzfunktion mit natürlichem Exponenten hat die Form
\(f\!: x \mapsto f(x) = x^n \ \ (n \in \mathbb N)\)
Ihr Funktionsgraph ist eine Parabel n-ter Ordnung, für n = 2 die Normalparabel. Die (maximale) Definitionsmenge ist \(D_f = \mathbb R\), der Wertebereich hängt von n ab: Bei geradem n ist \(W_f = \mathbb R_0^+\), bei ungeradem n ist \(W_f = \mathbb R\).
Die Potenzfunktion mit natürlichem Exponenten ist ein Spezialfall einer ganzrationalen Funktion (Polynomfunktion), bei der alle Koeffizienten außer einem null sind und dieser eine Koeffizient an = 1 ist.
Weitere Eigenschaften
-
Der Ursprung ist für alle Potenzfunktionen mit natürlichem Exponenten die einzige Nullstelle.
-
Parabeln von gerader Ordnung sind spiegelsymmetrisch zur y-Achse und damit gerade Funktionen (genau daher kommt diese Bezeichnung!), Parabeln von ungerader Ordnung sind ungerade Funktionen, also punktsymmetrisch zum Ursprung.
-
Gerade Parabeln haben im Ursprung einen Tiefpunkt, ungerade Parabeln einen Wendepunkt (außer für n = 1, dann ist der Graph die 1. Winkelhalbierende).