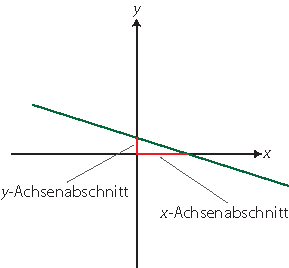
Der Achsenabschnitt ist der Abstand zwischen dem Schnittpunkt einer Linie mit einer Koordinatenachse und dem Nullpunkt bzw. Ursprung des Koordinatensystems. In der Analysis ist diese Linie ein Funktionsgraph,also z. B. eine Parabel oder eine Sinuskurve.
Beim Graphen einer linearen Funktion y = f(x) = mx + b entspricht der Parameter b dem y-Achsenabschnitt (er wird auch in der Regel so genannt). Allgemein ist der y-Achsenabschnitt der Funktionswert an der Stelle x = 0, also der Wert f(0). Der y-Achsenabschnitt ist für jede Funktion eindeutig bestimmt, da eine Funktion zu jedem x nur maximal einen Funktionswert haben darf (sonst wäre sie keine eindeutige Zuordnung).
Der Schnittpunkt eines Funktionsgraphen mit der x-Achse ist eine Nullstelle der Funktion. Da eine Funktion mehrere Nullstellen haben kann, ist der x-Achsenabschnitt im Allgemeinen nicht eindeutig bestimmt. Eine lineare Funktion hat allerdings nur eine Nullstelle (oder unendlich viele im Falle der Funktion f(x) = 0), sodass dort auch der x-Achsenabschnitt eindeutig bestimmt ist: \(\displaystyle f(x) = mx + b = 0 \ \ \Leftrightarrow \ \ x = -\frac b m\).
In der Analytischen Geometrie betrachtet man in der Regel die Achsenschnittpunkte von Geraden und Ebenen. Diese Punkte werden dort Spurpunkte genannt.