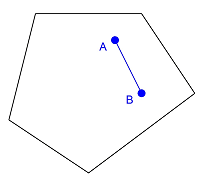
Eine konvexe Figur bzw. ein konvexer Körper besitzt weder „Einstülpungen“ noch Löcher. Dies bedeutet (und das ist auch die formale Definition), dass alle Verbindungslinien zwischen zwei Punkten der Figur oder des Körpers vollständig im Inneren liegen, man kann also immer „von A nach B“ kommen, ohne die Figur bzw. den Körper zu verlassen. Kurz: Eine Figur ist konvex, wenn sie mit je zwei Punkten A und B auch die Verbindungsstrecke \(\overline{AB}\) enthält.
Konvexe Figuren sind z. B. Dreiecke, Quadrate und alle anderen regelmäßigen Polygone sowie Kreise, konvexe Körper Würfel, Pyramiden oder Kugeln.
Das Gegenteil von konvex ist konkav.
In der Analysis nennt man Funktionsgraphen mit Rechtskrümmung konvex und Graphen mit Linkskrümmung konkav.