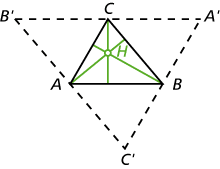
Die Höhe in einem Dreieck ist der senkrechte Abstand einer Ecke von der gegenüberliegenden Seite bzw. das Lot der Ecke auf diese Seite. Der Lotfußpunkt heißt in diesem Fall Höhenfußpunkt.
Die drei Höhen ha, hb und hc schneiden sich in einem Punkt, dem Höhenschnittpunkt H. Die Höhen in \(\triangle ABC\) sind gleichzeitig die Mittelsenkrechten (Mittellote) in \(\triangle A'B'C'\), das von den Parallelen zu den Seiten von \(\triangle ABC\) durch die Eckpunkte von \(\triangle ABC\) gebildet wird.
Die Höhe dient unter anderem zur Flächenberechnung: Die Fläche eines Dreiecks ist die Hälfte des Produkts aus einer Seite und der zugehörigen Höhe, \(\displaystyle A = \frac1 2 a\cdot h_a = \frac1 2 b\cdot h_b = \frac1 2 c\cdot h_c\).
In spitzwinkligen Dreiecken liegt der Höhenschnittpunkt H innerhalb, in stumpfwinkligen Dreiecken außerhalb des Dreiecks. Im rechtwinkligen Dreieck sind die beiden Katheten gleichzeitig Höhen; der Höhenschnittpunkt fällt mit dem Scheitel des rechten Winkels zusammen. Im gleichseitigen Dreieck fallen Höhen, Mittelsenkrechte, Seiten- und Winkelhalbierende sowie deren jeweilige Schnittpunkte zusammen.
Auch bei Vierecken spielt die Höhe eine Rolle, insbesondere bei der Flächenberechnung von Trapez (Höhe mal Mittelwert der parallelen Seiten) und Parallelogramm (Seite mal Höhe).
Auch bei einfachen Körpern wie Prisma und Zylinder bzw. Pyramide und Kegel kann man eine Höhe definieren. Diese ist in diesem Fall die Richtung, die senkrecht auf der Grundfläche steht (also die Normale auf der Grundfläche).