Was du wissen musst
-
Welche Eigenschaften von Kegelstümpfen sind wichtig?
Bei einem Kegelstumpf kannst du viele Größen berechnen. Das Volumen eines Kegelstumpfs wird dir immer wieder in Aufgaben begegnen. Das Volumen berechnest du mit der Formel:
\(V_{\text{Stumpf}}=\frac{1}{3} \cdot h \cdot \pi \cdot (r_1^2+r_1r_2+r_2^2)\)
Dabei bezeichnet \(h\) die Höhe des Kegelstumpfs, \(\pi\) die Kreiszahl, \(r_1\) den Radius der Deckfläche und \(r_2\) den Radius der Grundfläche. Dabei ist zu bedenken, dass der Radius aus dem Durchmesser \(d\) berechnet werden kann durch \(r_1=\frac{1}{2}\cdot d_1\) und \(r_2=\frac{1}{2}\cdot d_2\).
Wie dir bestimmt aufgefallen ist, besteht der Kegelstumpf aus vielen verschiedenen Flächen. Man unterscheidet die Grundfläche \(A_{\text {Grund}}\), die Deckfläche \(A_{\text{Deck}}\), die Mantelfläche \(A_M\) und die Gesamtfläche \(A_O\).
Die Grundfläche ist die Fläche, auf der der Kegelstumpf steht. Es ist eine Kreisfläche. Die Formel dafür lautet:\(A_{\text{Grund}}=\pi\cdot (r_2)^2\)
Ähnlich lässt sich auch die Deckfläche (auch Schnittfläche) berechnen:
\(A_{\text{Deck}}=\pi\cdot (r_1)^2\)
Die Grundfläche und die Deckfläche sind ähnlich zueinander.
Die Mantelfläche berechnet sich durch:
\(A_M=(r_1+r_2)\cdot \pi\cdot s\)
Dabei ist \(s\) die Mantellinie von dem Kegelstumpf.
Addiert man nun diese drei Flächen zueinander, erhält man die Gesamtfläche:
\(\begin{align}A_O&=A_{\text{Grund}}+A_{\text{Deck}}+A_M \\&=(\pi\cdot (r_2^2))+(\pi\cdot (r_1^2))+((r_1+r_2)\cdot \pi\cdot s)\end{align}\)
Eine wichtige Größe ist die Höhe. Diese berechnet sich mit folgender Formel:
\(h=\sqrt {s^2-(r_1-r_2)^2}\)
Vielleicht erkennst du den Satz des Pythagoras in der Formel. Die Formel kann nämlich grafisch genau mit diesem Hilfsmittel hergeleitet werden.
-
Welche Eigenschaften von Pyramidenstümpfen sind wichtig?
Grundsätzlich unterscheiden sich Pyramidenstümpfe genau wie Pyramiden durch ihre Grundflächen. Hier findest du die wichtigen Formeln für Pyramidenstümpfe mit quadratischen Grundflächen.
Das Volumen eines quadratischen Pyramidenstumpfs berechnest du mit der Formel:
\(V_{\text{Stumpf}}=\frac{1}{3} \cdot h \cdot (a^2+ab+b^2)\)
Dabei bezeichnet \(h\) die Höhe des Pyramidenstumpfs und \(a\) und \(b\) zwei beiden Seiten.
Genau wie der Kegelstumpf besteht der Pyramidenstumpf aus vielen verschiedenen Flächen. Man unterscheidet die Grundfläche \(A_{\text {Grund}}\), die Deckfläche (auch Schnittfläche) \(A_{\text{Deck}}\), die Mantelfläche \(A_M\) und die Gesamtfläche \(A_O\). Die Grundfläche und die Deckfläche sind ähnlich zueinander.
Die Grundfläche ist die Fläche, auf der der Pyramidenstumpf steht. Die Formel dafür lautet:
\(A_{\text{Grund}}=a^2\)
Analog lässt sich Deckfläche berechnen mit:
\(A_{\text{Deck}}=b^2\)
Die Mantelfläche berechnet sich durch:
\(A_M=2\cdot (a+b)\cdot s\)
Dabei ist \(s\) die Mantellinie des Pyramidenstumpfs.
Die Gesamtfläche setzt sich nun aus den Flächen zusammen:
\(\begin{align}A_O&=A_{\text{Grund}}+A_{\text{Deck}}+A_M \\&=a^2+b^2+2\cdot (a+b)\cdot s\end{align}\)
Eine weitere wichtige Größe ist die Höhe. Diese berechnet sich mit folgender Formel:
\(h=\frac{3\cdot V}{a^2+b^2+\sqrt{a\cdot b}}\)
Du musst bei Aufgaben zu diesem Thema besonders aufmerksam sein, denn ein Pyramidenstumpf hat viele verschiedene Arten, die je nach der Ausgangspyramide variieren.
-
Wie leitet man die Formeln für das Volumen des Kegelstumpfs her?
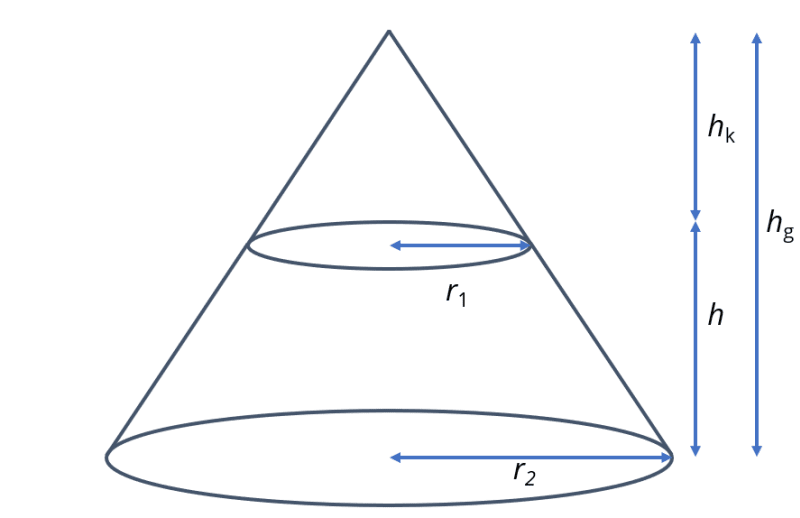
Die Grundidee dieses Beweises ist, dass du auf den Kegelstumpf noch einen weiteren Kegel setzt, der den gleichen Radius wie die Deckfläche des Kegelstumpfes hat. Dadurch entstehen zwei Kegel.
Durch die Strahlensätze gilt folgendes Verhältnis:
\(\frac{h_\text{k}}{r_1}=\frac{h_\text{g}}{r_2}=\frac{h_\text{k}+h}{r_2}\)
Dabei ist \(h_\text{g}=h_\text{k}+h\).
Durch Umformungen erhältst du die Formel für die Höhe des kleinen Kegels:
\(h_\text{k}=\frac{h}{r_2\cdot (\frac{1}{r_1}-\frac{1}{r_2})}\)
Das Volumen des Kegelstumpfs kann als Differenz des Volumens des großen Kegels und des Volumens des kleinen Kegels betrachtet werden. Du berechnest es mit der Formel:
\(V=\frac{1}{3}\cdot \pi\cdot h\)
Daraus entstehen die Kegelvolumina \(V_\text{k}\) und \(V_\text{g}\), die zur Berechnung des Volumens nötig sind:
\(\begin{align} V_{\text{Stumpf}}&= V_\text{g}-V_\text{k}\\&=\frac{1}{3}\pi \cdot r_2^2\cdot h_\text{g}-(\frac{1}{3}\pi \cdot r_1^2\cdot h_\text{k})\\&=\frac{1}{3}\pi \cdot (r_2^2\cdot h_\text{g}-r_1^2\cdot h_\text{k})\\&=\frac{1}{3}\pi \cdot (r_2^2\cdot (h+h_\text{k})-r_1^2\cdot h_\text{k})\\&=\frac{1}{3}\pi \cdot (r_2^2\cdot (h+\frac{h}{r_2\cdot (\frac{1}{r_1}-\frac{1}{r_2})}-r_1^2(\frac{h}{r_2\cdot (\frac{1}{r_1}-\frac{1}{r_2})})) \end{align}\)
Nun ziehst du \(h\) aus der Klammer und vereinfachst:
\(V_{\text{Stumpf}}=\frac{1}{3}\pi \cdot h\cdot (r_2^2+r_1\cdot (\frac{r_2^2}{r_2-r_1}-\frac{r_1^2}{r_2-r_1}))\)
Wende nun die dritte Binomische Formel an:
\(V_{\text{Stumpf}}=\frac{1}{3}\pi \cdot h\cdot (r_2^2+r_1\cdot (\frac{(r_2+r_1)(r_2-r_1)}{r_2-r_1}))\)
Daraus entsteht die gesamte Volumenformel für einen Kegelstumpf:
\(V_{\text{Stumpf}}=\frac{1}{3}\pi \cdot h\cdot (r_2^2+r_1r_2+r_1^2)\)
-
Wie leitet man die Formeln für das Volumen des Pyramidenstumpfs her?
Die Herleitung der Volumenformel für einen Pyramidenstumpf erfolgt ähnlich wie die Herleitung der Formel für den Kegelstumpf. Bei der ergänzten Pyramide ist die Grundfläche so groß wie die Schnittfläche des Pyramidenstumpfs.
Aus den Strahlensätzen erhältst du das Verhältnis:
\(\frac{h_\text{k}}{b^2}=\frac{h_\text{g}}{a^2}=\frac{h_\text{k}+h}{a^2}\)
Die Höhe der kleinen Pyramide kann berechnet werden mit:
\(h_\text{k}=\frac{h}{a^2\cdot (b^2-a^2)}\)
Nun wird das Volumen der kleinen Pyramide von dem Volumen der großen Pyramide abgezogen. Das Volumen einer Pyramide ermittelst du mit der Formel:
\(V=\frac{1}{3}\cdot a\cdot h\)
Daraus ergibt sich:
\(\begin{align} V_{\text{Stumpf}}&= V_\text{g}-V_\text{k}\\&=(\frac{1}{3}\cdot a\cdot h_\text{g})-(\frac{1}{3}\cdot b \cdot h_\text{k}) \end{align}\)
Durch Umformen kannst du nun die Formel des Volumens herleiten:
\(V_{\text{Stumpf}}=\frac{1}{3}\cdot h\cdot (a^2+ab+b^2)\)
-
Wozu benötigt man Kegelstümpfe?
Du brauchst das Körpernetz eines Kegelstumpfs zum Beispiel, um Mäntel zu nähen. Für das Schnittmuster ist die Mantelfläche des Kegelstumpfs relevant, da diese später das Hauptstück des genähten Mantels ergibt. Außerdem treten Kegelstümpfe häufig auch in Kunst oder Architektur auf.