• Aufgabe 1

    5 Minuten 2 Punkte
    einfach

    Ein Fußballfeld ist 110 m lang und 80 m breit. 

    1. Wie lange braucht der Platzwart, um den Rasen zu mähen, wenn er pro  Minute 2 a schafft?
    2. Wie lang ist die gesamte weiße Linie, die das Feld umrahmt?
    3. Wie groß ist die Fläche, in der der Torwart den Ball in die Hand nehmen darf, wenn der hierfür zulässige Strafraum 16,5 m breit und 40 m lang ist?

  • Aufgabe 2

    5 Minuten 4 Punkte
    einfach

    Schreibe jeweils in der angegebenen Einheit.

    1. 48 m² = ... cm²
    2. 4,25 cm³  = ... mm³
    3. 0,825 a = ... m²
    4. 5600 mm³ = ... ml

  • Aufgabe 3

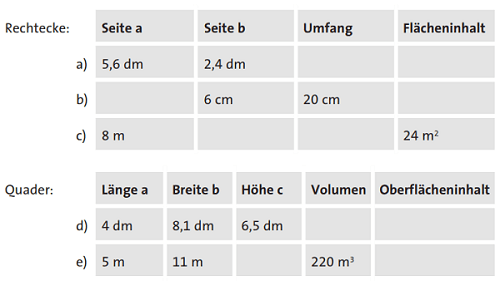
    10 Minuten 5 Punkte
    mittel

    Berechne die fehlenden Größen in den Tabellen. Rechne vorher in die nächstkleinere Einheit um, um die Kommaschreibweise zu umgehen.

     

  • Aufgabe 4

    7 Minuten 4 Punkte
    mittel

    Eine Stadt plant die Anlage eines Parkplatzes für 400 Pkw. Es werden für jedes Auto 10 m² benötigt und weitere 10 a für die Zufahrtswege.

    1. Wie viele Quadratmeter Fläche benötigt man für den Parkplatz? Wie viele Hektar sind das?
    2. Der rechteckige Parkplatz wird 100 m lang. Wie viel Meter ist die gesamte Umzäunung lang?

  • Aufgabe 5

    10 Minuten 6 Punkte
    mittel

    Hans kauft ein 80 cm langes, 40 cm breites und 30 cm hohes Aquarium. 

     

    Fische im Aquarium
    © Duden Learnattack GmbH

    1. Ein kleiner Zierfisch sollte mindestens 8 l Wasser zur Verfügung haben. Wie viele solcher Zierfische kann Hans in seinem Aquarium aufnehmen, wenn er es bis 5 cm unterhalb der Oberkante befüllt?
    2. Wie hoch steht das Wasser im Aquarium, wenn Hans einen ersten Eimer mit 10 l Fassungsvermögen hineingegossen hat? 
    3. Hans' Zimmer hat eine Grundfläche von 12 m². Wie hoch würde das Wasser stehen, falls das Aquarium einmal komplett auslaufen würde?
    4. Wie groß ist die Glasoberfläche des Aquariums, wenn der Boden aus einem anderen Material und das Aquarium oben offen ist?

  • Aufgabe 6

    8 Minuten 3 Punkte
    schwer

    Bearbeite die Textaufgabe.

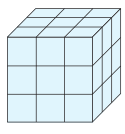
    Ein blau gestrichener Holzwürfel von 3 m Kantenlänge wird in 27 Würfel mit 1 m Kantenlänge zersägt. Beim Zersägen entstehen also kleine Würfel, deren Flächen nicht alle gestrichen sind. Wie groß ist die Gesamtfläche, die man nachstreichen muss, wenn auch die neuen Würfel wieder komplett blau sein sollen?