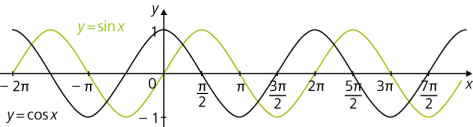
Die Sinusfunktion ist eine trigonometrische Funktion, welche den vom rechtwinkligen Dreieck bekannten Sinus eines Winkels („\(\sin \varphi\)“) zu einer auf ganz \(\mathbb R\) definierten Funktion erweitert. Dazu wird das Argument im Bogenmaß angegeben, also als Zahlenwert, wobei der rechte Winkel (±90°) dem Wert \(\displaystyle \pm \frac \pi 2\) und der Vollwinkel dem Wert \(2\pi\) entspricht.
Die Sinusfunktion ist periodisch, es gilt \(\sin x = \sin(x + k \cdot 2\pi) \ \ (k \in \mathbb Z)\).
Der Definitionsbereich ist, wie gesagt, \(D_f = \mathbb R\), der Wertebereich ist Wf = [–1; 1].
Der Funktionsgraph der Sinusfunktion ist punktsymmetrisch zum Urspung, sie ist also eine sog. ungerade Funktion. Er ist außerdem auch punktsymmetrisch zu allen Nullstellen (siehe unten) sowie spiegelsymmetrisch zu allen senkrechten Geraden durch die Extremstellen (jeweils weil die Funktion bis nach „\(\pm \infty\)“ periodisch ist).
Wenn man den Graphen der Sinusfunktion um \(\displaystyle \frac \pi 2\) nach links bzw. um \(\displaystyle \frac{3\pi}{2}\) nach rechts verschiebt, erhält man den Graphen der Kosinusfunktion.
Weitere Eigenschaften der Sinusfunktion
- Nullstellen: bei allen ganzzahligen Vielfachen von \(\pi\), also bei \(x_k = k \cdot \pi \ \ ( k \in \mathbb{Z})\)
- Extrema: lokale Maxima bei \(\displaystyle x_k = \left(2k + \frac 1 2\right) \cdot \pi\), lokale Minima bei \(\displaystyle x_k = \left(2k - \frac 1 2\right) \cdot \pi\), jeweils mit \(k \in \mathbb{Z}\).
- Monotonie: Zwischen den Extrema ist die Funktion jeweils streng monoton steigend bzw. fallend.
Die Ableitung der Sinusfunktion ist die Kosinusfunktion, ihre Stammfunktion ist die negative Sinusfunktion:
\((\sin x)' = \cos x\) und \(\int \sin x\,\text dx = -\cos x \ (+\ const.)\)