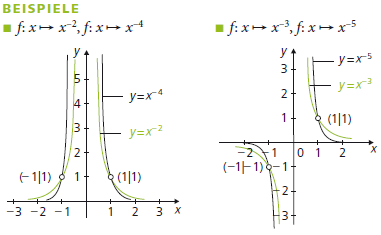Eine Potenzfunktion mit ganzzahlig negativem Exponenten ist definiert als
\(\displaystyle f\!: \mathbb R \setminus {0} \rightarrow \mathbb R \setminus {0}, \ \ x\mapsto x^{-n} \equiv \frac 1 {x^n} \ \ (n \in \mathbb N)\)
Manchmal sagt man auch „Hyperbelfunktion“ zu diesen Funktionen, dies ist aber missverständlich, da dies die Bezeichnung für die Funktionen Sinus hyperbolikus, Kosinus hyperbolikus und Tangens hyperbolikus ist (die allerdings in der Schule nur selten drankommen). Diese Sprechweise ist allerdings insofern verständlich, als dass für n = 1 der Funktionsgraph eine Hyperbel ist. Bei n > 1 spricht man manchmal auch von Hyperbeln n-ter Ordnung.
Eigenschaften
- Potenzfunktionen mit ganzzahlig negativem Exponenten haben keine Nullstelle.
- Für gerades n ist der Graph symmetrisch zur y-Achse, für ungerades n punktsymmetrisch zum Ursprung.
- Bei x = 0 hat der Graph eine Polstelle, wobei für ungerade n das Vorzeichen am Pol wechselt.
- Damit ist die y-Achse (Gerade x = 0) senkrechte Asymptote, die x-Achse ist waagerechte Asymptote.
- Für gerades n ist der Graph für x < 0 streng monoton steigend und für x > 0 streng monoton fallend. Bei ungeradem n fällt der Graph in der gesamten Definitionsmenge streng monoton.