Eine Hyperbel ist ein sog. Kegelschnitt, d. h. eine mathematische Kurve, die sich ergibt, wenn man die Exzentrizität einer Ellipse so weit steigert, dass sich die Figur gewissermaßen nicht mehr schließt (der Grenzfall zwischen Ellipse und Hyperbel ist die Parabel).
Man kann eine Hyperbel auch durch die folgende Gleichung definieren:
\(\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \ \ \Leftrightarrow \ \ y = \pm \frac b a x\cdot \sqrt{1 - \frac{a^2}{x^2}}\)
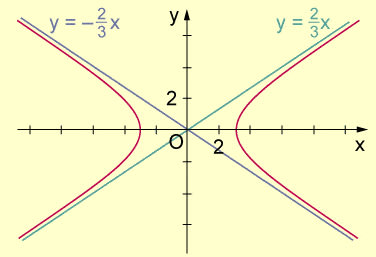
Das Zeichen „±“ deutet an, dass die Kurve aus zwei „Ästen“ besteht. Für \(x \rightarrow \pm \infty\) hat diese Kurve die Asymptoten \(\displaystyle y = \pm \frac b a x\).
Beispiel: a = 3, b = 2
Im Fall a = b = 1 sind dies die 1. und 2. Winkelhalbierende und die Kurve ist einfach eine um 45° gedrehte Version des Funktionsgraphen der antiproportionalen Zuordnung \(\displaystyle y = \frac 1 x\) bzw. der Potenzfunktion y = xn mit n = –1. In der Analysis meint man meistens diese Kurve, wenn von einer Hyperbel die Rede ist. Ihre Asymptoten sind die y- und die x-Achse.