Eine Zahlenfolge, bei welcher der Quotient \(\displaystyle q = \frac{a_{n+1}}{a_n}\) von zwei aufeinanderfolgenden Gliedern für alle \(n \in \mathbb N\) gleich groß (konstant) ist, nennt man einen geometische Zahlenfolge.
Die Bezeichnung „geometische Zahlenfolge“ rührt daher, dass von drei aufeinanderfolgenden Gliedern an–1, an und an+1 das mittlere Glied an immer gleich dem geometischen Mittel der beiden äußeren Glieder ist: \(\displaystyle a_n = \sqrt{a_{n-1} \cdot a_{n + 1}}\ (n \in \mathbb{N})\).
Für arithmetische Zahlenfolgen gilt das explizite Bildungsgesetz: an = a1 · qn–1 (\(n \in \mathbb{N}\)).
Beispiele:
- (an) = 0,25; 0,5; 1; 2; 4; 8; … explizites Bildungsgesetz an = 0,25 · 2n–1, oder rekursiv definiert: a1 = 0,25 und an+1 = an · 2.
- (an) = \(\displaystyle (a_n) = 3; - 1; \frac{1}{3} ; - \frac{1}{9} ; \frac{1}{27} ;\ \ldots\), mit dem Bildungsgesetz \(\displaystyle a_n = 3 \cdot \left( - \frac{1}{3} \right)^{n - 1} \ (\ n \in \mathbb{N})\) also \(\displaystyle q = - \frac{1}{3}\), rekursiv definiert: \(\displaystyle a_1 = 3, \ a_{n + 1} = - \frac{1}{3} \cdot a_n\) .
Ein bekanntes Beispiel kommt aus der Zinsrechnung: Der Zinsesins am Ende aufeinander folgender Finanzjahre bildet eine geometrische Zahlenfolge.
Wenn q > 1 und a1 > 0 ist, nimmt die geometrische Zahlenfolge streng monoton zu, bei q = 1 ist sie konstant und für 0 < q < 1 und a1 > 0 nimmt sie streng monoton ab und ist nach unten beschränkt.
Wenn q negativ ist, ist die geometrische Folge alternierend, wechselt also mit jedem Glied das Vorzeichen.
Die Punkte Pn(n|an), die den Funktionsgraphen einer geometischen Zahlenfolge bilden, liegen für q > 1 und a1 > 0
auf der Geraden mit der Gleichung y = f(x) = d · x + (a1 – d), und zwar immer bei ganzzahlig-positiven x-Werten.
Eine geometrische Zahlenfolge mit \(a_n = a_1 \cdot q^{n - 1} ;\ n \in \mathbb{N}\)
- ist für \(q > 1\) und \(a_1 > 0\) streng monoton zunehmend,
- ist für \(q = 1\) konstant und
- ist für \(0 < q < 1\) und \(a_1 > 0\) streng monoton abnehmend und nach unten beschränkt.
Die Punkte \(P_n (n| a n ),\ n \in \mathbb{N}\), die den Graphen einer geometrischen Zahlenfolge mit \(a_n = a_1 \cdot q^{n - 1}\) bilden, liegen für \(a_1 > 0\) und \(q > 0\) auf einer Exponentialkurve mit der Gleichung \(\displaystyle y = a_1 \cdot q^{x-1}= \frac{a_1}{q} \cdot q^x \ (x \in \mathbb{R})\).
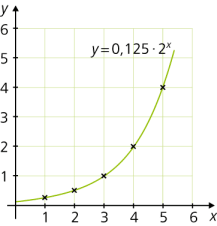
Beispiel:
Die Punkte von \(a_n = 0,25 \cdot 2^{n - 1}\) liegen auf dem Funktionsgraphen der Funktion \(y = 0,125 \cdot 2^x\):