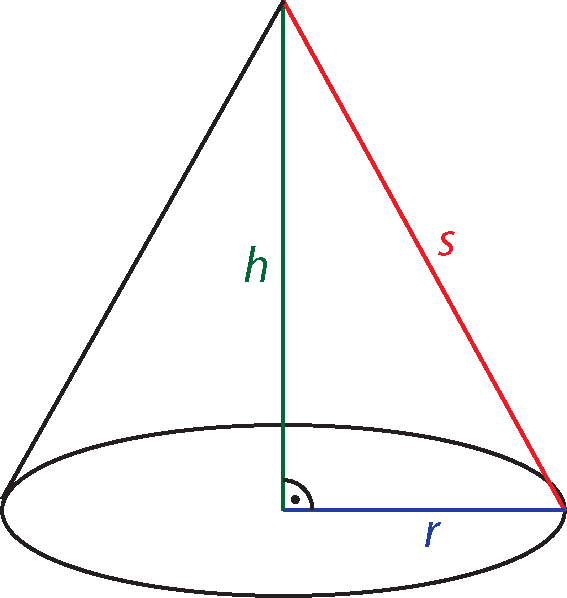
Ein (gerader) Kegel ist ein Rotationskörper, der entsteht, wenn man ein rechtwinkliges Dreieck um eine seiner Katheten im Raum rotiert.
Die Höhe h des Kegels ist die Länge der Kathete, um die rotiert wird. Die Grundfläche ist ein Kreis mit der Länge r der anderen Kathete als Radius und der Fläche \(G = \pi r^2\). Die Mantellinie s des Kegels ist die Hypotenuse des Dreiecks, mit dem Pythagoras-Satz gilt:
r2 + h2 = s2
Für das Volumen des Kegels gilt die Formel \(\displaystyle V = \frac 1 3 \cdot G \cdot h = \frac 1 3 \pi r^2 h \), also genau wie bei der Pyramide „Grundfläche mal Höhe durch 3“.
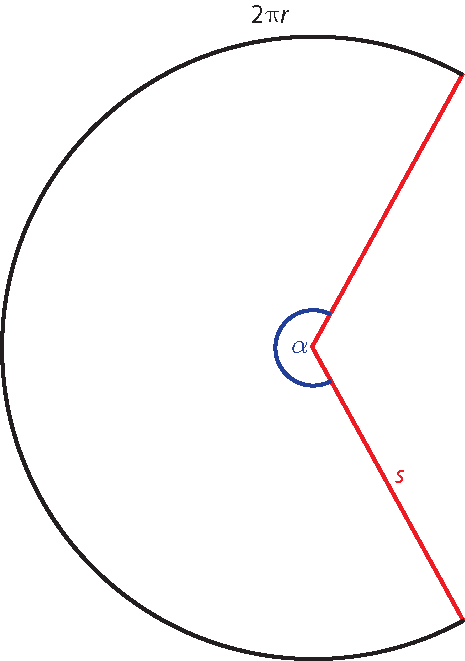
Die Oberfläche setzt sich aus der Grundfläche G und der Mantelfläche M zusammen. Letztere bestimmt man, indem man die Mantefläche in Gedanken „abrollt“. Diese wird dann zu einem Kreissektor mit Radius s und Bogenlänge \(2\pi r\). Die Größe des Winkels \(\alpha\) im Bogenmaß ist \(\displaystyle \alpha = \frac{2\pi r}{s}\) und für die Mantelfläche AM gilt:
\(\displaystyle A_\text M = \frac{\alpha}{2\pi} \cdot \pi s^2 = \pi rs\)
Also hat der Kegel die Oberfläche
\(A_\text{Kegel} = \pi r^2 + \pi r s = \pi r(r+s)\)
Bei einem schiefen Kegel (Schiefkegel) steht die Höhe nicht senkrecht auf dem Grundkreis, also liegt die Spitze des Kegel auch nicht über dem Grundkreismittelpunkt. Die Volumenformel \(\displaystyle V = \frac 1 3 \cdot G \cdot h = \frac 1 3 \pi r^2 h \) gilt dann immer noch, die Mantelfläche muss dann allerdings mit einem komplizierten Integral berechnet werden.
