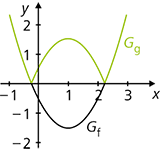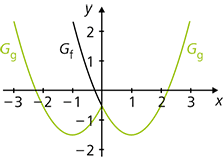Form- und Lageänderungen von Funktionsgraphen

Bei der Kurvendiskussion beschäftigt man sich nicht nur mit den Symmetrien von Funktionsgraphen, sondern auch mit einfachen geometrischen Abbildungen, durch die Graphen z. B. verschoben, gespiegelt, gestreckt oder gestaucht werden können. Solche Form- und Lageänderungen kann man oft direkt an einem Parameter im Funktionsterm ablesen. Durch Variation des Paramters erhält man eine Funktionenschar bzw. Kurvenschar und spricht daher auch von Parameterfunktionen – ganz ähnlich wie bei einer Geradenschar bzw. Ebenenschar in der Analytischen Geometrie.

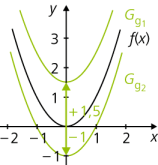
• Eine vertikale Verschiebung des Funktionsgraphen erreicht man durch Addition einer Konstanten zum Funktionsterm: g(x) = f(x) + a. Wenn die Konstante positiv ist (a > 0), verschiebt sich der Graph von f, G_f, nach oben, wenn sie negativ ist (a < 0), nach unten.
  Beispiel:
  f(x) = x², g₁(x) = x² + 1,5 und g₂(x) = x² – 1​
  

  

  
   
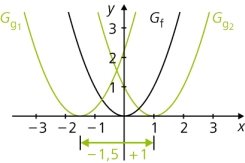
• Eine horizontale Verschiebung des Funktionsgraphen erreicht man durch Addition einer Konstanten zum Argument der Funktion (also zur unabhängigen Variablen, die man meistens x nennt): g(x) = f(x + b). Wenn die Konstante positiv ist (b > 0), verschiebt sich der Graph nach links, d. h. in negative x-Richtung, wenn sie negativ ist (b < 0), nach rechts, also in Richtung positiver x-Werte. 
  Beispiel:
  f(x) = x², g₁(x) = (x + 1,5)² und g₂(x) = (x – 1​)²
  

  

  
   
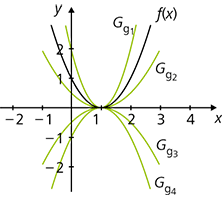
• Eine vertikale Streckung oder Stauchung des Funktionsgraphen erreicht man, indem man den Funktionsterm mit einer Konstanten multipliziert: g(x) = c · f(x) (\(c \ne 0\)). Dabei ändern sich die Nullstellen der Funktion nicht. Für |c| > 1 wird der Graph gestreckt, bei |c| < 1 gestaucht. Wenn die Konstante c negativ ist, wird der Graph außerdem noch an der x-Achse gespiegelt. 
  Beispiel:
  f(x) = (x – 1)², g₁(x) = 2(x – 1)², g₂(x) = 0,5(x – 1)², g₃(x) = –0,5(x – 1)² und g₄(x) = –(x – 1)²​
  

  

  
  Beachte: Die Graphen zu y₁ = c · f(x) und y₂ =  –c · f(x) sind zueinander spiegelsymmetrisch bezüglich der x-Achse.
   
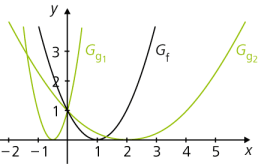
• Eine horizontale Streckung oder Stauchung des Funktionsgraphen erreicht man, indem man das Argument mit einer Konstanten multipliziert: g(x) = f(d · x) (\(d \ne 0\)). Dabei ändert sich der y-Achsenabschnitt nicht. Für |d| > 1 wird der Graph gestaucht, bei |d| < 1 gestreckt, der Streckfaktor ist jeweils \(\displaystyle \left| \frac 1 d \right|\). Wenn die Konstante d negativ ist, wird der Graph außerdem noch an der y-Achse gespiegelt.
  Beispiel:
  f(x) = (x – 1)², g₁(x) = (–2x – 1)² und g₂(x) = (0,5x – 1)²
  

  

  
  Beachte: Die Graphen zu y₁ = f(d · x) und y₂ =  f(–d · x) sind zueinander spiegelsymmetrisch bezüglich der y-Achse.
   
• Wenn man den Betrag des Funktionsterms, g(x) = |f(x)| bzw. den Betrag des Arguments, g(x) = f(|x|), einsetzt, wird der unter der x-Achse bzw. der rechts von der y-Achse liegende Teil des Funktionsgraphen gespiegelt. Im ersten Fall bleiben die Nullstellen, im zweiten Fall der y-Achsenabschnitt erhalten.

  Beispiele:

  
  f(x) = x² – 2x – 0,5 und  g(x) = |x² – 2x – 0,5|
  

  

  f(x) = x² – 2x – 0,5 und  g(x) = |x|² – 2|x| – 0,5