Die Parameterform ist eine Möglichkeit, Geraden oder Ebenen durch eine Vektorgleichung darzustellen. Dabei ist in der Regel ein Punkt bekannt, der Aufpunkt, sowie ein Richtungsvektor der gesuchten Geraden bzw. zwei Spannvektoren der gesuchten Ebene. Man sagt daher manchmal auch „Punkt-Richtungs-Form“ zu dieser Darstellung.
Man kann eine Ebenengleichung in Parameterform relativ einfach in die Koordinatenform umwandeln (für Geraden funktioniert das ganz ähnlich, nur mit einer Komponente weniger).
Beispiel:
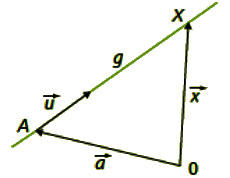
Eine Gerade g wird beschrieben durch den Aufpunkt A, zu dessen Ortsvektor \(\vec a\), zu dem ein positives oder negatives Vielfaches \(\lambda\) des Richtungsvektors \(\vec u\) addiert wird. In der Skizze ist der Faktor für den Punkt X etwa \(\lambda = 2,8\).
Allgemein lautet die Gleichung für die Gerade g
\(g: \ \vec x = \vec a + \lambda \cdot \vec u\) bzw. \(g: \ \begin{pmatrix} x_1 \\x_2\end{pmatrix} = \begin{pmatrix} a_1 \\a_2\end{pmatrix} + \lambda \cdot \begin{pmatrix} u_1 \\u_2\end{pmatrix} = \begin{pmatrix} a_1 + \lambda \cdot u_1\\ a_2 + \lambda \cdot u_2 \end{pmatrix}\)
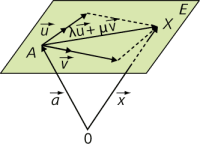
Bei einer Ebenen gibt es zwei Spannvektoren und daher auch zwei Parameter \(\lambda\) und \(\mu\):
\(E: \ \vec x = \vec a + \lambda \cdot \vec u + \mu \cdot \vec v\) bzw. \(E: \ \begin{pmatrix} x_1 \\x_2\\x_3\end{pmatrix} = \begin{pmatrix} a_1 \\a_2\\a_3\end{pmatrix} + \lambda \cdot \begin{pmatrix} u_1 \\u_2\\u_3 \end{pmatrix} + \mu \cdot \begin{pmatrix} v_1 \\v_2\\v_3 \end{pmatrix} = \begin{pmatrix} a_1 + \lambda \cdot u_1 + \mu \cdot u_1\\ a_2 + \lambda \cdot u_2+ \mu \cdot u_2 \\ a_3 + \lambda \cdot u_3+ \mu \cdot u_3 \end{pmatrix}\)
Eine Variante der Parameterform ist die Zweipunkteform (bei Geraden) bzw. die Dreipunkteform (bei Ebenen), deren Namen ziemlich selbsterklärend sind.