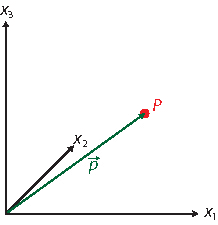
Ein Ortsvektor ist ein Vektor, der vom Ursprung O des (kartesischen) Koordinatensystems zu einem Punkt P in der Ebene bzw. im Raum zeigt: \(\vec p = \overrightarrow{OP}\). Anders als bei allgemeinen Vektoren ist also bei einem Ortsvektor der Startpunkt festgelegt und außerdem abhängig vom gewählten Koordinatenursprung: \(\vec p' = \overrightarrow{O'P} \ne \vec p = \overrightarrow{OP}\).
Die Komponenten des Ortsvektors \(\vec p = \begin{pmatrix} p_1 \\ p_2 \end{pmatrix}\) eines Punkts P(p1|p2) in der Ebene bzw. \(\vec p = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix}\) eines Punkts P(p1|p2|p3) im Raum entsprechen gerade den Koordinaten dieses Punkts, weswegen oft nicht klar zwischen Punkt und Ortsvektor unterschieden wird. Trotzdem sollte man sich die Mühe machen, hier klar zu trennen – ein Punkt ist eine ausdehnungslose Position in der Eben oder dem Raum, ein Vektor besitzt eine Richtung und einen Betrag, also eine Länge.