Die Normalform (auch Normalenform) ist eine Möglichkeit, Geraden oder Ebenen durch eine Vektorgleichung darzustellen. Sie bietet sich dann an, wenn bereits ein Normalenvektor bekannt ist.
Hat eine Gerade oder Ebene den Normalenvektor \(\vec n\), dann gilt für alle Punkte der Gerade bzw. der Ebene
\(\vec n \circ \vec x = k\)
denn der Normalenvektor steht definitionsgemäß auf allen Punkten der Geraden bzw. Ebene gleichermaßen senkrecht, also ist das Skalarprodukt mit ihm für alle Punkte bzw. deren Ortsvektoren gleich groß.
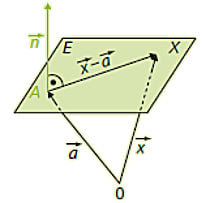
Eine alternative Form verwendet einen Aufpunkt (Stützvektor) \(\vec a\). Da der Differenzvektor \(\vec a - \vec x\) in der Ebene liegt, steht \(\vec n\) auf ihm senkrecht und das Skalarprodukt verschwindet:
\(\vec n \circ \left( \vec x - \vec a \right) = 0\)
Einen Spezialfall stellt die Hesse’sche Normalform dar, bei welcher der Normalenvektor zusätzlich noch normiert ist, also ein Einheitsvektor mit dem Betrag 1 ist.