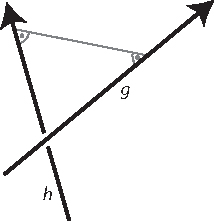
Zwei Geraden heißen windschief, wenn sie weder parallel sind noch einen Schnittpunkt haben. Dies ist nur im dreidimensionalen Raum möglich, in der Ebene schneiden sich nicht parallele Geraden immer.
Ein Kriterium dafür, dass zwei Geraden im Raum zueinander windschief stehen, ist, dass beide Richtungsvektoren und der Differenzvektor (Verbindungsvektor) eines beliebigen Punkts auf der einen Geraden und eines Punkts auf der anderen voneinander linear unabhängig sind.
Beispiel:
\(g\! : \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix} \ \ ( \lambda \in \mathbb{R})\) und \(h\!: \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ -4 \\ -2 \end{pmatrix} \ \ ( \mu \in \mathbb{R})\)
Sind die beiden Richtungsvektoren und der Verbindungsvektor \(\begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} - \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix}\) linear unabhängig?
\(\det \left( \begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix}; \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix}; \begin{pmatrix} 4-1 \\ 3-3 \\ 1-5 \end{pmatrix} \right) = \begin{vmatrix} 3 & -3 & 3 \\ 2 & -4 & 0 \\ 1 & 2 & -4 \end{vmatrix} = 3 \cdot (- 4) \cdot (- 4) + (-3) \cdot 0 \cdot 1 + 3 \cdot 2 \cdot 2 - 1 \cdot (- 4) \cdot 3 - 2 \cdot 0 \cdot 3 - (- 4) \cdot 2 \cdot (- 3) = 48 \neq 0\)
Die Determinante ist ungleich 0, also sind g und h tatsächlich windschief.