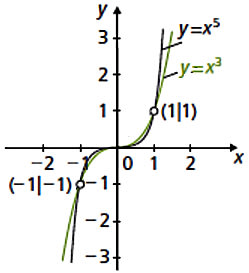Ein Funktionsgraph hat einen Sattelpunkt oder Terrassenpunkt, wenn er an einer Stelle gleichzeitig einen Wendepunkt und eine waagerechte Tangente besitzt. Dies bedeutet für die notwendige Bedingung, dass dort sowohl die erste als auch die zweite Ableitung der Funktion verschwinden (null sind).
Gerne wird als hinreichende Bedingung gefordert, dass die dritte Ableitung nicht null sein darf. Sicherer ist aber die hinreichende Bedingung, dass sich das Vorzeichen der zweiten Ableitung kurz vor und kurz nach dem möglichen Sattelpunkt verändert.
Ein typisches Beispiel sind Potenzfunktionen mit ungeradem natürlichem Exponenten, y = xn (n > 1). Diese haben alle im Ursprung einen Sattelpunkt. Die Abbilung zeigt y = x3 und y = x5. Bei y = x3 genügt die hinreichende Bedingung mit der dritten Ableitung, um den Punkt nachzuweisen; bei y = x5 wird das Vorzeichenkriterium über die zweite Ableitung benötigt.