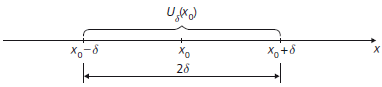
In der Analysis ist eine Umgebung \(U_{x_0}\) bzw. U(x0) um eine Zahl x0 das offene Intervall \(]x_0 - \delta; \ x_0 + \delta[ \ \ (\delta>0)\). x0 liegt somit exakt in der Mitte des Intervalls. Wenn es auf die Intervallbreite. also einen bestimmten Wert von \(\delta\) ankommt, sagt man auch \(\delta\)-Umgebung (\(U_\delta(x_0)\)).
Die „punktierte \(\delta\)-Umgebung“ ist das Intervall ohne den Punkt x0 selbst, also \(U_\delta \setminus \{x_0\}\).
Umgebungen werden bei der Untersuchung von Ableitungen und anderen Grenzwerten von Funktionen benötigt.